The Least-squares Trend Line calculator computes the regression line, a linear equation, through a set of X and Y values.  This is also known as simple linear regression. The Least-square Equation produces this linear equation in the form y = a + bx.

INSTRUCTIONS: Enter the following:

• (X,Y)  Tabular Data of X,Y pairs (see Example right)
• (OC) Output Choice (Trend Line, Details)

Least-squares Trend Line (Y = a + bX): The calculator computes the Least-square Trend Line, correlation coefficient (r) and supporting calculation details:

• (n) Number of Pairs
• (MX) Mean of X values
• (MY) Mean of Y values
• (ΣX) Sum of X values
• (ΣY) Sum of  Y values
• (ΣXY) Sum of X⋅Y values
• (ΣX²) Sum of X² values
• (ΣY²) Sum of Y² values

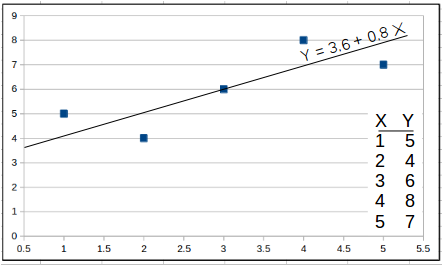
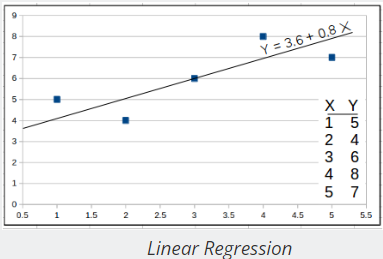
Example in Graphic

If you want the find the least squares trend line through 

INPUTS

1,5
2,4
3,6
4,8
5,7

The calculator will return "Y = 3.6 + 0.8X".

The Math / Science

The formula for the least-squared regression line is in the following form:

y = a + bx

             where:

                          `b = (  (sum(XY) - (sumX * sumY)"/n")) / (sum(X^2) - (sumX)^2"/n") `
             and
                            ` a = MY - b*MX`           MY is mean of Y.  MX is mean of X.

Correlation

To determine if there is a correlation between X and Y, the calculator computes the correlation coefficient (r). The range of r is -1 ≤ r ≤ 1, with the strongest correlations the further one gets from zero, either negative or positive. The formula for the correlation coefficient (r) is as follows:

     `r = b * (sum(X^2)- sum(X)^2"/n")/(sum(Y^2)- sum(Y)^2"/n")`

Linear Equations

• Compute the Slope-Intercept form of a Line based on two points
• Compute the slope between two points
• Linear Equation
• Distance between a Point and Line
• Compute the Least-squares Linear Regression Equation
• Constant of Proportionality
• Constant of Inverse Proportionality

Statistics Calculators

• Observational Stats:  This function accepts a table (rows and columns separated by commas) of numbers and calculates observational statistics for any of the columns.  This includes count, min, max, sum, sum of squares (Σx²), square of the sum (Σx)², mean, median, mode, range, mid point, rand, sort up, sort down, rand, population variance, population standard deviation, the sample/experimental variance, sample/experimental standard deviation.
• Simple Stats: This is also provides a full set of observational stats, but on a single row of numbers separated by commas. The observational stats include count, min, max, sum, sum of squares (Σx²), square of the sum (Σx)², mean, median, mode, range, mid point, rand, sort up, sort down, rand, population variance, population standard deviation, the sample/experimental variance, sample/experimental standard deviation.
• Frequency Distribution:  This function lets you enter a string of numbers separated by commas, a low and high range and a number of bins.  It then computes how many of the observations are in each of the bins between the high and low values designated. 
• Paired Sample t-test:  This computes the various parameters associated with the Paired Sample t-test.
• ANOVA (one way): The computes the F Score and details for one way analysis of variance for a nxm matrix of observations.
• (χ²) Chi-Square Test: This computes the Chi-Square value for an nxm array of data and provides the degrees of freedom.
• Linear Regression:  This computes the regression line (least-squares) through a set of X and Y observations.  It also computes the regression coefficient (r).
• Least-squares Trend Inference :  This is a linear equation used with Linear Regression to compute a predicted value of Y based on X.
• Wilcoxon Signed Rank Test: This provides the Wilcoxon statistics and critical value for two groups of numeric observations based on an alpha value and whether it's a one or two tailed test.
• Slope-Intercept form of a Line: This provides the slope intercept form (y = mx+b) of a line based on two coordinates.
• Slope between two points: This provides the slope between two coordinates.
• Linear Equation: This computes the range (y) of a linear equation (y = mx +b) and includes a graphing function.
• Probability between z SCORES: 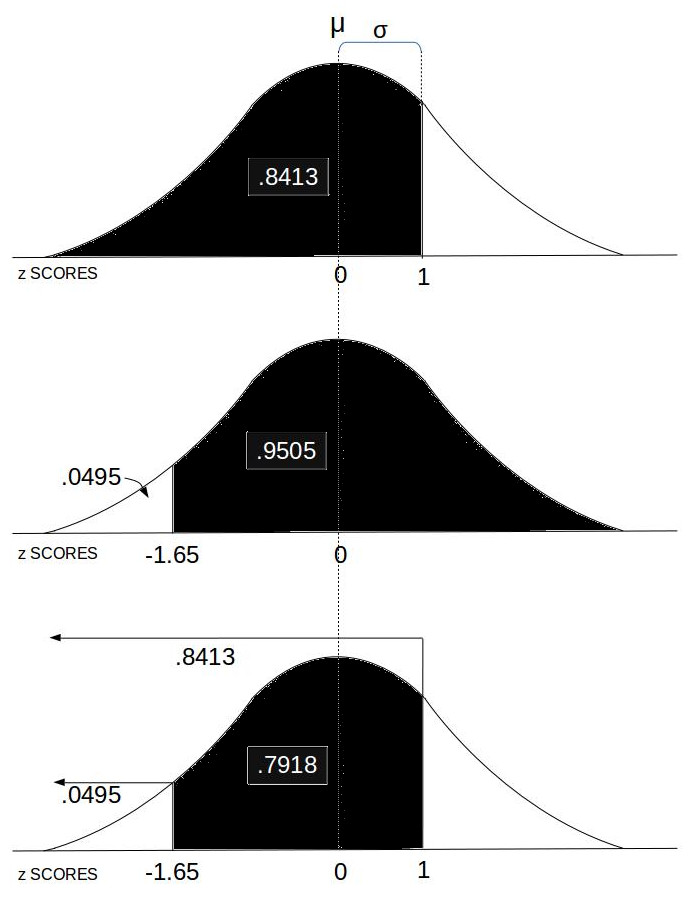This computes the area under the Normal Distribution curve between two z SCOREs which equates to the probability of an event in that range.
• Stats Calc: College level statistics calculator with a bundle including most of the functions in this list.
• Count: This computes the number (n) of observations in a set of numbers.
• Minimum: This computes the minimum (min) value in a set of numbers.
• Maximum: This computes the maximum (max) value in a set of numbers.
• Numeric Sort: This sorts (ascending or descending) a set of comma separated numerical observations.
• Random Sample (k items): The provides a random subset of a specified size (k) in a set of comma separated numerical observations.
• Random Real Number in Range: The provides a random real number between two specified real numbers (upper and lower bounds).
• Radom Integer: The provides a random integer between two specified integers (upper and lower bounds).
• Frequency Distribution: This provides a frequency distribution table for a comma separated set of numbers with a specified number of frequency bins between a lower and upper data range. 
• Sum (Σx): This is computes the sum of the values in a set.
• Sum of Squares (Σx²): This computes the sum of the squared values in a set.
• Sum Squared (Σx)²:  This computes the square of the summed values in a set.
• Mean (μ): This computes is the mean (average) of values in a set.
• Median: This identifies the middle ordered value in a set of numbers.
• Statistical Mode: This identifies the most recurring observation in a set of numbers.
• Mid Point: This is identifies the mid point of the observation range in a set of numbers.
• Range: This is computes the difference between the max and the min values in a set of number.
• Population Variance (σ²): This computes the variance, a metric regarding the spread of values, for a population set of numeric values.
• Population Standard Deviation (σ):  This computes the standard deviation for a population set of numeric values.
• Sample Variance (s²) : This computes the variance, a metric regarding the spread of values, for a sample set of numeric values within a greater population.
• Sample Standard Deviation (s): This computes the standard deviation for a sample set of numeric values within a greater population.
• z SCORE Formula: This computes the z SCORE for a value base on the mean and standard deviation.
• z SCORE: This computes the z SCORE for a value (Raw Score) based on a set of values, and whether that set is sample or population. 
• Percentile: This computes the percentile of a value (y) in a set (X) of values.
• Standard Deviation of Mean (SDOM):  This computes the standard deviation of mean, sometimes also known as the standard error of the mean (SEM), useful to helps quantify the uncertainty in the estimate of the mean.  
• Percent Relative Standard Deviation (%RSD): This computes the percent relative standard deviation, also known as the coefficient of variation (CV).  The %RSD is a measure of the dispersion of a probability distribution.

References

•  Dowdy, Shirley, and Stanley Wearden. Statistics for Research. N.p.: John Wiley & Sons, n.d. Print.(Chapter 9 Distributions of Paired Variables)