The Vector Calculator (3D) computes vector functions (e.g. V • U and V x U) VECTORS in 3D Vector Angle (between vectors)
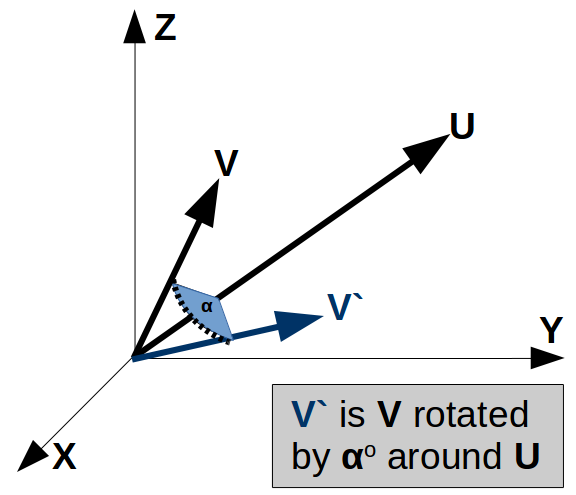 Vector Rotation
Vector Rotation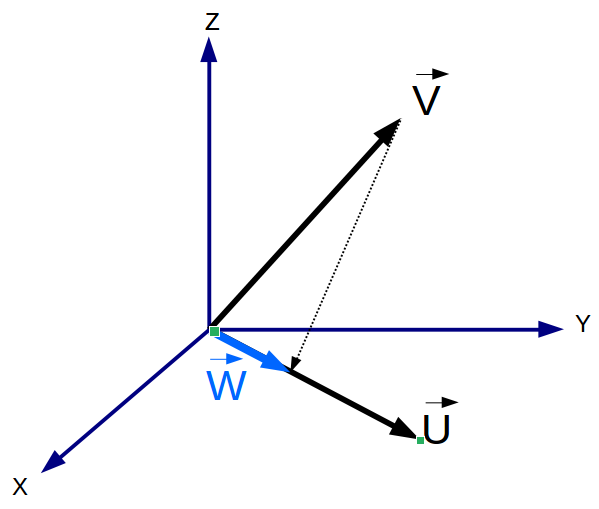 Vector Projection in three dimensional (3D) space.
Vector Projection in three dimensional (3D) space.
3D Vector Calculator Functions:
- k V - scalar multiplication
- V / |V| - Computes the Unit Vector
- |V| - Computes the magnitude of a vector
- U + V - Vector addition
- U - V - Vector subtraction
- |U - V| - Distance between vector endpoints.
- |U + V| - Magnitude of vector sum.
- V • U - Computes the dot product of two vectors
- V x U - Computes the cross product of two vectors
- V x U • W - Computes the mixed product of three vectors
- Vector Angle - Computes the angle between two vectors
- Vector Area - Computes the area between two vectors
- Vector Projection - Compute the vector projection of V onto U.
- Vector Rotation - Compute the result vector after rotating around an axis.
- Normal to 3 Points - Vector Normal to a Plane Defined by Three Points
- (ρ, θ, φ) to (x,y,z) - Spherical to Cartesian coordinates
- (x,y,z) to (ρ, θ, φ) - Cartesian to Spherical coordinates
- (r, θ, z) to (x,y,z) - Cylindrical to Cartesian coordinates
- (x,y,z) to (r, θ, z) - Cartesian to Cylindrical coordinates
- Vector Components - Magnitude, Unit Vector and angle between vector and three coordinate axes
NOTE: Previously, all vectors are entered and returned in comma separated form (e.g., 3.45,5.97,-1.34). This was to facilitate cut/copy/paste between vector functions which helps you string together functions as needed. However, to ease user inputs, vector boxes are being used in several functions.
Related Items:
- For a YouTube video with instructions on how to use the calculator (CLICK HERE).
- For vectors in Physics, see Light and Matter (Dr. Benjamin Crowell):
- CLICK HERE for a Quaternion Calculator.
Dot Product (V • U)
In mathematics, the dot product, or scalar product (or sometimes inner product in the context of Euclidean space), is an algebraic operation that takes two equal-length sequences of numbers (usually coordinate vectors) and returns a single number. This operation can be defined either algebraically or geometrically. Algebraically, it is the sum of the products of the corresponding entries of the two sequences of numbers. 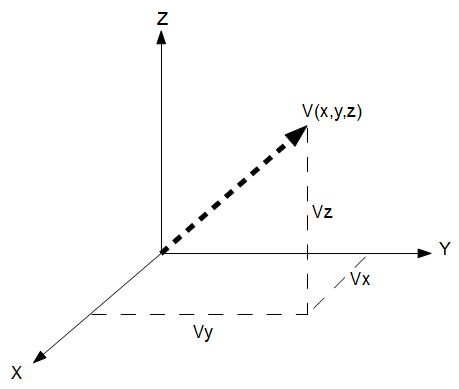 Cartesian (XYZ) Coordinates
Cartesian (XYZ) Coordinates 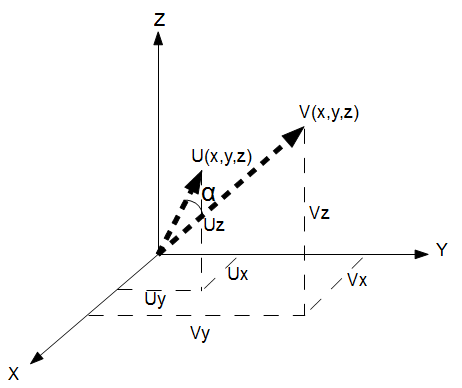 Two vectors in 3D
Two vectors in 3D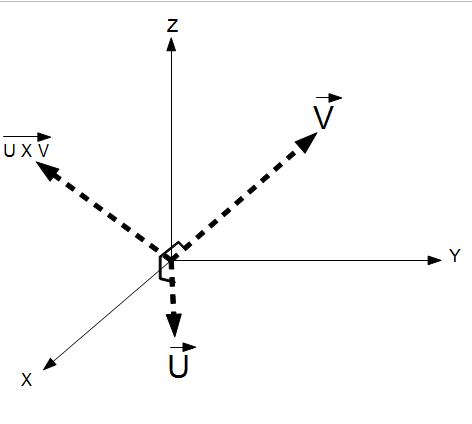 Vector Cross Product
Vector Cross Product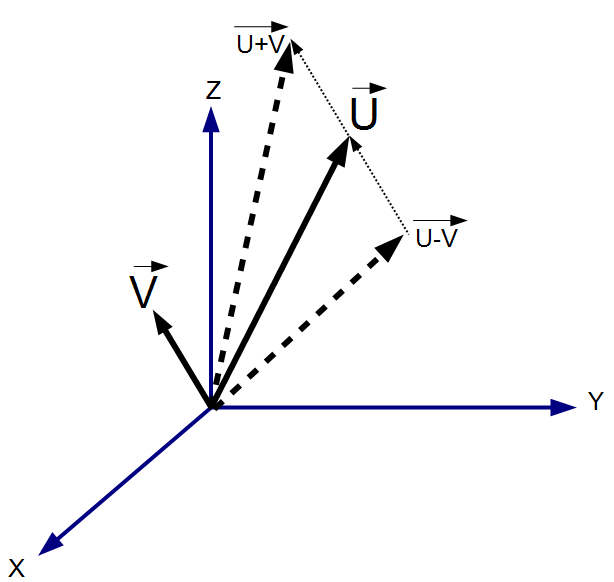 vector addition and subtraction Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. The name "dot product" is derived from the centered dot " · " that is often used to designate this operation; the alternative name "scalar product" emphasizes the scalar (rather than vectorial) nature of the result.
vector addition and subtraction Geometrically, it is the product of the Euclidean magnitudes of the two vectors and the cosine of the angle between them. The name "dot product" is derived from the centered dot " · " that is often used to designate this operation; the alternative name "scalar product" emphasizes the scalar (rather than vectorial) nature of the result.
This calculator uses the arc-cosine of the dot product to calculate the angle between two vectors after it has converted the vectors into unit vectors. Note: the arc-cosine (cosine inverse) of the dot product of two non-unit vectors does not produce the angle between them.
Cross Product (V x U)
In mathematics, the cross product or vector product is a binary operation on two vectors in three-dimensional space and is denoted by the symbol ×. The cross product a × b of the vectors a and b is a vector that is perpendicular to both and therefore normal to the plane containing them. It has many applications in mathematics, physics, and engineering.
If the vectors have the same direction or one has zero length, then their cross product is zero. More generally, the magnitude of the product equals the area of a parallelogram with the vectors for sides; in particular, for perpendicular vectors, this is a rectangle and the magnitude of the product is the product of their lengths. The cross product is anticommutative (i.e. a × b = −b × a) and is distributive over addition (i.e. a × (b + c) = a × b + a × c). The space and product form an algebra over a field, which is neither commutative nor associative, but is a Lie algebra with the cross product being the Lie bracket.
Like the dot product, it depends on the metric of Euclidean space, but unlike the dot product, it also depends on a choice of orientation or "handedness". The product can be generalized in various ways; it can be made independent of orientation by changing the result to pseudovector, or in arbitrary dimensions the exterior product of vectors can be used with a bivector or two-form result. Also, using the orientation and metric structure just as for the traditional 3-dimensional cross product, one can in n dimensions take the product of n − 1 vectors to produce a vector perpendicular to all of them. But if the product is limited to non-trivial binary products with vector results, it exists only in three and seven dimensions.
Right Hand Convention: Note that cross product depicted in the diagram has the order of U X V, where U is first. This diagram shows the right and convention. Consider placing one's right hand along the first vector in the operation (U in the diagram). If one then sweeps the hand counter clockwise (normal right hand motion) towards the second vector (V in the diagram), the resulting normal vector (U X V) will be in the direction of one's extended thumb, hence the "Right Hand Convention".
Vector addition and subtraction (V +/- U)
The sum of two vectors (V, U) is the vector that results in the sum of the their respective components, such that U + V = (Ux+Vx, Uy+Vy, Uz+Vz). This can be seen visually (see diagram), by placing the origin of the second vector on the tip of the first. The resulting vector goes from the origin of the first vector and the tip of the second vector.
The difference of two vectors (V, U) is the vector that results in the difference of the their respective components, such that U - V = (Ux-Vx, Uy-Vy, Uz-Vz). This can be seen visually (see diagram), by placing the tip (as opposed to the origin) of the second vector on the tip of the first. The resulting vector goes from the origin of the first vector and the origin of the second vector.
Vector Rotation
A common function in 3D vectors is to perform a rotation about an axis. This is used in aerospace for things like attitude control in satellites and animation such as where an animated character's gun pointing (e.g. Woody in Toy Story). This Vector Rotation function uses quaternions to compute the result of the rotation of a vector (V) about an axis defined by another vector (U) for a prescribed angle (α). This rotation operates according to the "right hand rule". To understand this, think of the rotation vector (U) as the thumb on your right hand, and your index finger as the vector (V). The rotation angle is the counter-clockwise motion of your index finger during the rotation. Thanks to Damon Ostrander and Tom Sathre for their help with the quaternion math. CLICK HERE for Quaternion Calculator
Vector Projection
The vector projection of a vector V onto a nonzero vector U (also known as the vector component or vector resolution of V in the direction of U) is the orthogonal projection of V onto a straight line parallel to U. 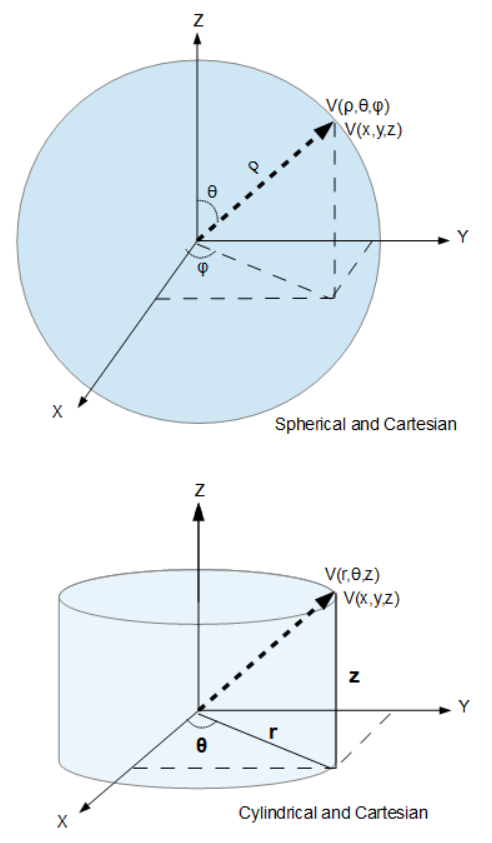 Spherical and Cylindrical
Spherical and Cylindrical
Spherical Coordinates
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuth angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane.
The radial distance is also called the radius or radial coordinate. The polar angle may be called co-latitude, zenith angle, normal angle, or inclination angle.
The use of symbols and the order of the coordinates differs between sources. In one system frequently encountered in physics (ρ, θ, φ) gives the radial distance, polar angle, and azimuthal angle, whereas in another system used in many mathematics books (ρ, θ, φ) gives the radial distance, azimuthal angle, and polar angle. In both systems ρ is often used instead of r. Other conventions are also used, so great care needs to be taken to check which one is being used.
A number of different spherical coordinate systems following other conventions are used outside mathematics. In a geographical coordinate system positions are measured in latitude, longitude and height or altitude. There are a number of different celestial coordinate systems based on different fundamental planes and with different terms for the various coordinates. The spherical coordinate systems used in mathematics normally use radians rather than degrees and measure the azimuthal angle counter-clockwise rather than clockwise[further explanation needed]. The inclination angle is often replaced by the elevation angle measured from the reference plane. Elevation angle of zero is at the horizon.
The spherical coordinate system generalizes the two-dimensional polar coordinate system. It can also be extended to higher-dimensional spaces and is then referred to as a hyperspherical coordinate system.
Cylindrical Coordinates
In mathematics, a cylindrical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers:
- (r) the radius of the base of the cylinder (r) with the center at the region that also intersects with the point,
- (θ) the angle from the origin to the x,y plane (θ), and
- (z) the elevation above or below the x,y plane (z)
University Contributors to vCalc
See Also
- Quaternion Calculator - suite of quaternion functions
- Matrix Multiplication - Suite of Matrix functions
- Circular Motion - Physics calculator with equations related to circular motion.
- Projectile Motion - Physics calculator with equations related to projectile motion.
- Physics 100- Physics calculator and units converter
- Physics 105 - Physics calculator
- Astro Travel Time - time equation for travel to astronomical objects from Earth at different velocities.
- Force of Drag - Drag force equation and data
- Pendulum - Calculator with equations for the pendulum.
Flight and Navigation Calculators
- Correction Angle: Computes the navigation angle/azimuth correction angle using the wind speed, wind direction, flight heading and an Air Speed.
- Ground Speed: Computes the ground speed based on the wind speed, wind direction, a Flight Heading and an Air Speed.
- Haversine - Distance: Computes the distance between two points on a spherical model of the Earth along a great circle arc. This also includes the rhumb line distance and azimuth for the rhumb line.
- Travel Time between Coordinates: Computes the time to travel between to points on the globe in a great circle arc at an average velocity.
- Distance to Sea Level Horizon at Altitude: Computes the distance to the horizon from a specified height using a spherical model the mean spherical radius of the Earth
- Force of Drag: Calculates the resisting force of drag on an object flowing through a medium (e.g. air).
- Force of Lift: Computes the lifting force on the surface area of a wing based on the wing surface area, air flow velocity, density of air and a lift coefficient.
- Lift Coefficient: Compute the lift coefficient of a wing based on lift force, wing surface area, wind speed and density of air.
- Velocity Needed for Takeoff: Computes the velocity required to create more lift than the weight of an aircraft or watercraft using a wing (e.g. hydrofoil).
- Glide Ratio: Computes the glide ratio based on the change in forward distance and the change in altitude.
- Wing Surface Area: Computes the wing surface area required to achieve lift, base on a lift coefficient, lift force, wind speed and density of air.
- Velocity of Air over the Wing: Computes the velocity required to achieve a lift, based on lift coefficient, lift force, wing surface area and density of air.
- Air Speed from Pressures: It uses the Bernoulli Equation to estimate air speed based on the total Pressure measured by a pilot tube, total Static local atmospheric pressure and the Density of Air.
- Center of Mass: Computes the vehicle center of mass between two loads (masses).
- Cloud Base: Estimates the height above the ground of the cloud base from the Dew Point and Surface Temperature.
