The Spherical to Cartesian formula calculates the cartesian coordinates 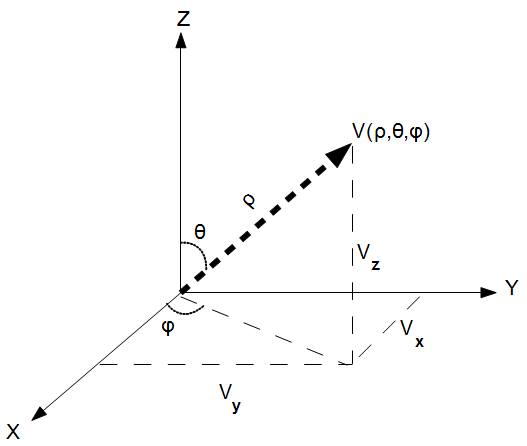 Vector in 3D for a vector give its Spherical coordinates.
Vector in 3D for a vector give its Spherical coordinates.
INSTRUCTIONS: Choose units and enter the following:
- (ρ) magnitude of vector
- (Θ) polar angle (angle from z-axis)
- (φ) azimuth angle (angle from x-axis)
Cartesian Coordinates (x, y, z): The calculator returns the cartesian coordinates as real numbers.
Spherical Coordinates
In mathematics, a spherical coordinate system is a coordinate system for three-dimensional space where the position of a point is specified by three numbers: the radial distance of that point from a fixed origin, its polar angle measured from a fixed zenith direction, and the azimuth angle of its orthogonal projection on a reference plane that passes through the origin and is orthogonal to the zenith, measured from a fixed reference direction on that plane.
The radial distance is also called the radius or radial coordinate. The polar angle may be called co-latitude, zenith angle, normal angle, or inclination angle.
The use of symbols and the order of the coordinates differs between sources. In one system frequently encountered in physics (r, θ, φ) gives the radial distance, polar angle, and azimuthal angle, whereas in another system used in many mathematics books (r, θ, φ) gives the radial distance, azimuthal angle, and polar angle. In both systems ρ is often used instead of r. Other conventions are also used, so great care needs to be taken to check which one is being used.
A number of different spherical coordinate systems following other conventions are used outside mathematics. In a geographical coordinate system positions are measured in latitude, longitude and height or altitude. There are a number of different celestial coordinate systems based on different fundamental planes and with different terms for the various coordinates. The spherical coordinate systems used in mathematics normally use radians rather than degrees and measure the azimuthal angle counter-clockwise rather than clockwise[further explanation needed]. The inclination angle is often replaced by the elevation angle measured from the reference plane. Elevation angle of zero is at the horizon.
The spherical coordinate system generalizes the two-dimensional polar coordinate system. It can also be extended to higher-dimensional spaces and is then referred to as a hyperspherical coordinate system.
Definition
To define a spherical coordinate system, one must choose two orthogonal directions, the zenith and the azimuth reference, and an origin point in space. These choices determine a reference plane that contains the origin and is perpendicular to the zenith. The spherical coordinates of a point P are then defined as follows:
The radius or radial distance is the Euclidean distance from the origin O to P.
The inclination (or polar angle) is the angle between the zenith direction and the line segment OP.
The azimuth (or azimuthal angle) is the signed angle measured from the azimuth reference direction to the orthogonal projection of the line segment OP on the reference plane.
The sign of the azimuth is determined by choosing what is a positive sense of turning about the zenith. This choice is arbitrary, and is part of the coordinate system's definition.
The elevation angle is 90 degrees (π/2 radians) minus the inclination angle.
If the inclination is zero or 180 degrees (π radians), the azimuth is arbitrary. If the radius is zero, both azimuth and inclination are arbitrary.
In linear algebra, the vector from the origin O to the point P is often called the position vector of P.
Conventions
Several different conventions exist for representing the three coordinates, and for the order in which they should be written. The use of (r, θ, φ) to denote radial distance, inclination (or elevation), and azimuth, respectively, is common practice in physics, and is specified by ISO standard 80000-2 :2009, and earlier in ISO 31-11 (1992).
However, some authors (including mathematicians) use φ for inclination (or elevation) and θ for azimuth, which "provides a logical extension of the usual polar coordinates notation". Some authors may also list the azimuth before the inclination (or elevation), and/or use ρ (rho) instead of r for radial distance. Some combinations of these choices result in a left-handed coordinate system. The standard convention (r, θ, φ) conflicts with the usual notation for the two-dimensional polar coordinates, where θ is often used for the azimuth. It may also conflict with the notation used for three-dimensional cylindrical coordinates.
The angles are typically measured in degrees (°) or radians (rad), where 360° = 2π rad. Degrees are most common in geography, astronomy, and engineering, whereas radians are commonly used in mathematics and theoretical physics. The unit for radial distance is usually determined by the context.
When the system is used for physical three-space, it is customary to use positive sign for azimuth angles that are measured in the counter-clockwise sense from the reference direction on the reference plane, as seen from the zenith side of the plane. This convention is used, in particular, for geographical coordinates, where the "zenith" direction is north and positive azimuth (longitude) angles are measured eastwards from some prime meridian.
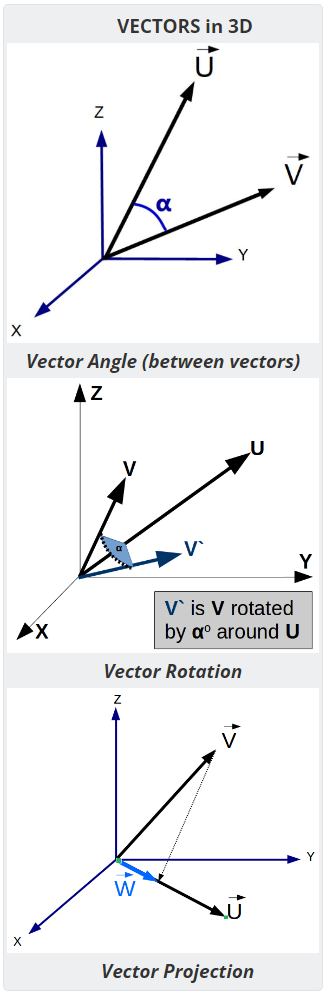
3D Vector Functions
 k⋅V - scalar multiplication
k⋅V - scalar multiplication- V/k - scalar division
- V / |V| - Computes the Unit Vector
- |V| - Computes the magnitude of a vector
- U + V - Vector addition
- U - V - Vector subtraction
- |U - V| - Distance between vector endpoints.
- |U + V| - Magnitude of vector sum.
- V • U - Computes the dot product of two vectors
- V x U - Computes the cross product of two vectors
- V x U • W - Computes the mixed product of three vectors
- Vector Angle - Computes the angle between two vectors
- Vector Area - Computes the area between two vectors
- Vector Projection - Compute the vector projection of V onto U.
- Vector Rotation - Compute the result vector after rotating around an axis.
- Vector Components 3D - Returns a vector's magnitude, unit vector, spherical coordinates, cylindrical coordinates and angle from each axis.
- (ρ, θ, φ) to (x,y,z) - Spherical to Cartesian coordinates
- (x,y,z) to (ρ, θ, φ) - Cartesian to Spherical coordinates
- (r, θ, z) to (x,y,z) - Cylindrical to Cartesian coordinates
- (x,y,z) to (r, θ, z) - Cartesian to Cylindrical coordinates
- (x,y) to (r, θ) - Cartesian to Polar
- (r, θ) to (x,y) - Polar to Cartesian
- Vector Normal to a Plane Defined by Three Points
References
- Light and Matter by Benjamin Crowell, Chapter 7.1 Vector Notation
- Wikipedia - http://en.wikipedia.org/wiki/Spherical_coordinate_system
