The Vector Area calculator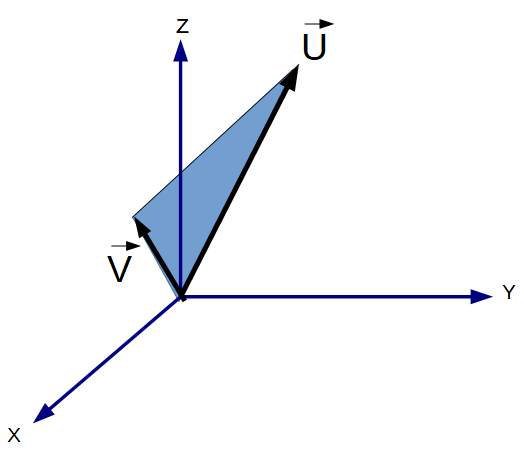 Vectors U and V in three dimensions computes the area swept between two vectors (V and U) in Euclidean three dimensional space. This is the light blue area in the graphic.
Vectors U and V in three dimensions computes the area swept between two vectors (V and U) in Euclidean three dimensional space. This is the light blue area in the graphic.
INSTRUCTIONS: Enter the following in meters:
- (V): Vector V in meters
- (U): Vector U in meters
Area between Vectors (A): The calculator returns area in square meters. However, this can be automatically converted to compatible units via the pull-down menu.
The Math / Science
The Area between two Vectors (A) calculator computes the two dimensional area between two 3D vectors. The formula to compute the area is:
- Compute the length (magnitude) of both vectors. They represent the length of two legs of a triangle (|V| and |U|).
- Compute the angle between the vectors(α).
- Use the two lengths of and the angle to compute the area of the triangle, where:
A = 1/2 ⋅ |V| ⋅ |U| ⋅ sin(α)
This formula lets the user enter two three-dimensional vectors (V and U) with X, Y and Z components. Note the dot product of two unit vectors is equal to the cosine of the angle between the two vectors.
3D Vector Functions
 k⋅V - scalar multiplication
k⋅V - scalar multiplication- V/k - scalar division
- V / |V| - Computes the Unit Vector
- |V| - Computes the magnitude of a vector
- U + V - Vector addition
- U - V - Vector subtraction
- |U - V| - Distance between vector endpoints.
- |U + V| - Magnitude of vector sum.
- V • U - Computes the dot product of two vectors
- V x U - Computes the cross product of two vectors
- V x U • W - Computes the mixed product of three vectors
- Vector Angle - Computes the angle between two vectors
- Vector Area - Computes the area between two vectors
- Vector Projection - Compute the vector projection of V onto U.
- Vector Rotation - Compute the result vector after rotating around an axis.
- Vector Components 3D - Returns a vector's magnitude, unit vector, spherical coordinates, cylindrical coordinates and angle from each axis.
- (ρ, θ, φ) to (x,y,z) - Spherical to Cartesian coordinates
- (x,y,z) to (ρ, θ, φ) - Cartesian to Spherical coordinates
- (r, θ, z) to (x,y,z) - Cylindrical to Cartesian coordinates
- (x,y,z) to (r, θ, z) - Cartesian to Cylindrical coordinates
- (x,y) to (r, θ) - Cartesian to Polar
- (r, θ) to (x,y) - Polar to Cartesian
- Vector Normal to a Plane Defined by Three Points
A triangle is a polygon with three sides, three vertices (corners), and three angles. Triangles can be classified based on the lengths of their sides and the measures of their angles as follows:
By Side Lengths:
- Equilateral Triangle: All three sides are equal in length.
- Isosceles Triangle: Two sides are equal in length.
- Scalene Triangle: All three sides have different lengths.
By Angle Measures:
- Acute Triangle: All three angles are less than 90 degrees.
- Right Triangle: One angle is exactly 90 degrees.
- Obtuse Triangle: One angle is greater than 90 degrees.
The sum of the interior angles of any triangle always adds up to 180 degrees.
Triangle Calculators
- Area of Triangle (base and height)
- Area of Triangle (two sides and interior angle)
- Area of Triangle (two angles and interior side)
- Area of Triangle (three sides)
- Area of Equilateral Triangle
- Area of Triangle (three points)
- Height of Triangle
- Width of Triangle
- Triangle Perimeter
- Interior Angle of a triangle based on the length of three sides
- Semi-perimeter of a triangle
- Area of Circle Within a Triangle
- Area of Circle Around a Triangle
- Area between two vectors
- Triangle Volume
