Processing...
`alpha = "acos"(hatV*hatU)`
Enter a value for all fields
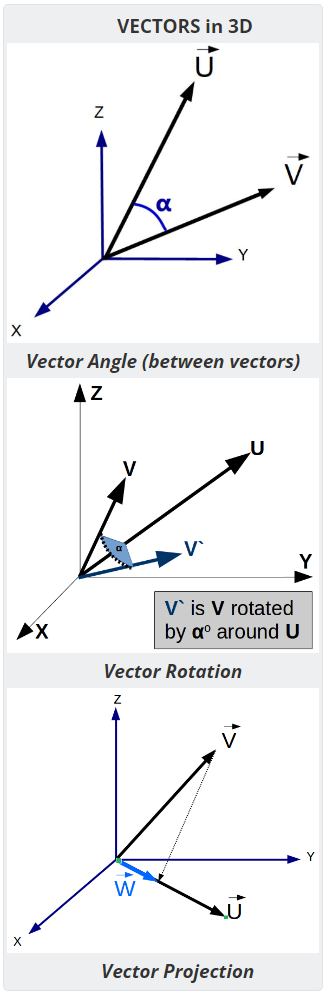
The Angle Between Vectors calculator computes the angle(α) separating two vectors (V and U) in three dimensional space.
INSTRUCTIONS: Enter the following:
- (V): Vector V
- (U): Vector U
Angle Between Vectors (α): The calculator returns the angle (α) between the two vectors in degrees and radians. However, these can be automatically converted into compatible units via the pull-down menu.
The Math / Science
The angle between vectors formula lets the user enter two three-dimensional vectors (V and U) with X, Y and Z components (Euclidean 3-space vectors).
α = acos(`hatU * hatV`)
where:
- α = angle between `vecV` and `vecU`
- `hatU` = unit vector for `vecU`
- `hatV` = unit vector for `vecV`
To calculate the angle between two vectors:
- calculate the unit vectors associated with vector V and vector U. To do that,
- compute the magnitude of the vectors and then
- do a scalar multiplication for each of the vectors where the scalar(k) is the inverse of the vector's magnitude.
- calculate the dot product of the unit vectors
- calculate the arc-cosine of that dot product to calculate the angle between the vectors in radians.
- converts radians to degrees.
3D Vector Functions
 k⋅V - scalar multiplication
k⋅V - scalar multiplication- V/k - scalar division
- V / |V| - Computes the Unit Vector
- |V| - Computes the magnitude of a vector
- U + V - Vector addition
- U - V - Vector subtraction
- |U - V| - Distance between vector endpoints.
- |U + V| - Magnitude of vector sum.
- V • U - Computes the dot product of two vectors
- V x U - Computes the cross product of two vectors
- V x U • W - Computes the mixed product of three vectors
- Vector Angle - Computes the angle between two vectors
- Vector Area - Computes the area between two vectors
- Vector Projection - Compute the vector projection of V onto U.
- Vector Rotation - Compute the result vector after rotating around an axis.
- Vector Components 3D - Returns a vector's magnitude, unit vector, spherical coordinates, cylindrical coordinates and angle from each axis.
- (ρ, θ, φ) to (x,y,z) - Spherical to Cartesian coordinates
- (x,y,z) to (ρ, θ, φ) - Cartesian to Spherical coordinates
- (r, θ, z) to (x,y,z) - Cylindrical to Cartesian coordinates
- (x,y,z) to (r, θ, z) - Cartesian to Cylindrical coordinates
- (x,y) to (r, θ) - Cartesian to Polar
- (r, θ) to (x,y) - Polar to Cartesian
- Vector Normal to a Plane Defined by Three Points
