The Volume of a Cylinder calculator computes the volume of a right circular cylinder from the height (h) and radius (r).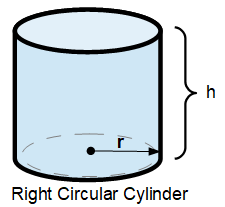
INSTRUCTIONS: Choose units and enter the following:
- (r) Radius of Cylinder
- (h) Height of Cylinder
Volume of a Cylinder (V): The calculator returns the volume (V) in cubic meters. However, this can be automatically converted to many other volume units (e.g. cubic inches) via the pull-down menu.
The Math
The formula for the volume of a cylinder is:
V = π•r²•h
where:
- V is the volume of the cylinder
- r is the Radius of the cylinder .
- h is the Height of the cylinder.

Cylinder Calculators
- Cylinder Side Area: Computes the surface area of the sides of a cylinder based on height and radius.

- Cylinder Surface Area: Computes the total surface area of a cylinder including sides, top and bottom.
- Cylinder Volume: Computes the volume of a cylinder based on cylinder height and radius.
- Cylinder Volume from Height and Circumference: Computes the volume of a cylinder based on the height and circumference. It also returns the diameter of the cylinder.
- Cylinder Height: Computes the height of a cylinder based on the volume and radius.
- Cylinder Radius: Computes the radius and diameter of a cylinder based on the volume and height.
- Cylinder Weight: Computes the weight, mass and volume of a cylinder based on the height, radius and density.
- Cylinder Mass Computes the mass of a cylinder based on the radius and height and mean density of the cylinder.
- Volume in Horizontal Cylinder: Computes partial volume of a horizontal circular cylinder based on the radius and length of the cylinder and the vertical height of the contents in the cylinder (see diagram).
- Cylinder Density: Computes the mean density of a cylinder based on the mass and computed volume from the radius and height.
- Slanted Cylinder Surface Area: Computes the surface area of a slanted cylinder based on the radius and side length (L).
- Slanted Cylinder Area from Angle: Computes the lateral area (surface area of the sides) of a slanted cylinder based on its radius, height and slant angle (θ).
- Slanted Cylinder Volume: Computes the volume of a slanted cylinder based on the radius of the base, side length and slant angle.
- Slanted Cylinder Weight: Computes the weight or mass of a slanted cylinder based on the radius, side length, slant angle and density.
- Cylinder MoI about Central Axis: Computes the moment of inertia of a cylinder about its central axis based on the mass and radius.
- Cylinder MoI about the End: Computes the moment of inertia of a solid circular cylinder of uniform density about an axis along the diameter of the cylinder at one end.
- Cylinder MoI Perpendicular to Axis: Computes the moment of inertia of a solid circular cylinder of uniform density about an axis perpendicular to the axis of the cylinder and through the center of mass.
Volume is a three dimensional measurement of the amount of space taken up by an object. Volume units are cubic measurements for solid objects such as cubic inches and cubic meters. Fluids have separate volume units such as liters, fluid ounces, cups, gallons, and barrel.
The volume of an object can measured by the liquid it displaces or be calculated by measuring its dimensions and applying those dimensions to a formula describing its shape. Many such calculations are available in the following list of calculators.
In many cases, the calculators are for a column with a geometric shaped base and vertical sides. One basic formula for volume is area times a Height when the volume has vertical sides.
Volume Calculators
- Volume from Area and Height
- Volume of a Cube
- Volume of a Box
- Volume of a Cone
- Volume of a Cone Frustum
- Volume of a Cylinder
- Volume of a Slanted Cylinder
- Volume of a Semicircle
- Volume of a Triangular
- Volume of a Quadrilateral
- Volume of a Pentagon
- Volume of a Hexagon
- Volume of a Heptagon
- Volume of a Octagon
- Volume of a Nonagon
- Volume of a Decagon
- Volume of a Hendecagon
- Volume of a Dodecagon
- Volume of a Paraboloid
- Volume of a Polygon based Pyramid
- Volume of a Pyramid Frustum
- Volume of a Sphere
- Volume of a Sphere Cap
- Volume of a Sphere Segment
- Volume of a Sphere Shell
- Volume of a Oblate Spheroid
- Volume of a Ellipsoid
- Volume of a Torus
- Volume of a Bottle
- Volume of a Chamfer
- Gasket Volume
Plumbing Calculators
- Rolling Offsets (Run and Travel) – The Rolling Offset
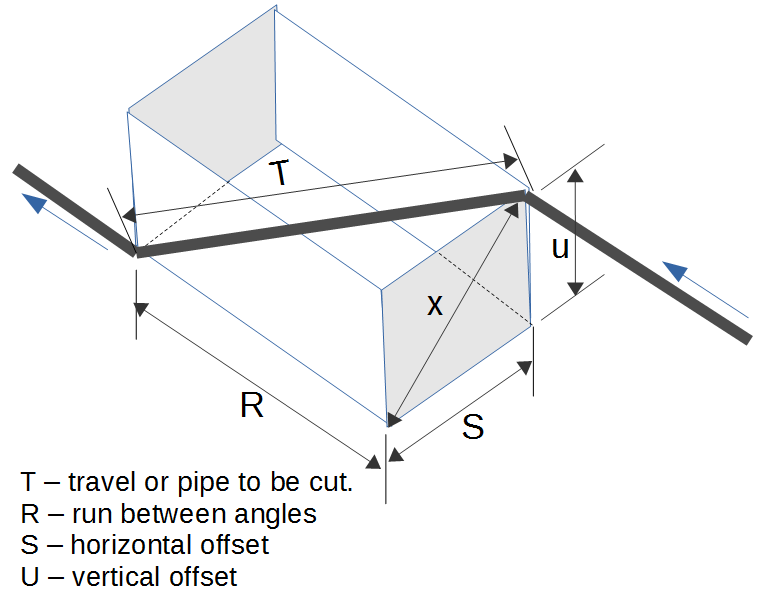 Rolling Offset Lengths
Rolling Offset Lengths Pipe Grading function computes the run and travel length a rolling offset based on the offsets and fittings. (see diagram).
- Pipe Grading - Compute the drop needed over a run to maintain a grade (e.g., 4" over 12')
- Diagonal of a Square - This is a simple calculation to assist in computing the diagonal of a square.
- Diagonal of a Box - This computes the length of the diagonal of a box (T) based on sides of length R, S and U.
- Flow Rate - This computes flow rate based on the total volume and the time it took to accumulate.
- Pipe Flow Volume - This computes the total volume from a pipe based on the flow rated and the duration of flow.
- Weight of Water in a Tank
- Computes the weight of water in a cylindrical tank based on the radius and height (or length).
- Weight of Water in a Pipe - Computes the weight of water or other substances in a pipe based on the dimension and material density.
- Weight of Sea Water in pipe - Computes the weight of sea water in a cylinder based on the radius and height (or length)
- Pressure Head - The Potential Gravity-Fed Water Pressure from a Tank (a.k.a. Pressure Head) based on the height of storage.
- Pipe Volume - Computes the volume in a pipe.
- Pipe Surface Area - Computes the surface area of a pipe.
- Pipe Coating Amount - Computes the volume of coating material for a pipe such as paint, polyethylene, polyurethane, zinc, bitumen, FBE or mortar.
- Volume of Water in a Tank (e.g. hot water tanks),
- Volume of a Spherical Container
- Weight of Water in a Spherical Container
- Volume of Water in Rectangular Tank
- Weight of Water in a Rectangular Tank
- Capillary Rise - The height of water in a small tube due to capillary force.
- Snow Water Equivalence - The volume of water created by an area and depth of snow.
- Pore Water Pressure - Pressure of uplift from the water table.
- Pipe Stress Budget - Computes the pressure that a pipe can withstand based on the allowable stress, wall thickness and outside diameter.
- Water in Basement Volume: Computes the volume of water in an area such as a basement based on the dimensions and the time required to pump it out based on a sump pump rate.
- Paint for Pipes: Computes the amount of paint needed to cover the exterior surface area of one or more pipes based on the pipe diameter, length, number of coats, number of pipes and the recommended area coverage of the paint.
- Time to Fill: Computes the amount of time necessary to fill something (e.g., tank or pool) based on the volume and flow rate.
- Pipe Insulation Calc: Computes the number of bags of pipe insulation needed for a run of pipes based on the 12' of length per bag and the length of pipe run to be insulated.
- Head Height: Computes the head height of liquid needed to achieve a pressure for a liquid (default is water).