The Volume of an Oblate Spheroid equation (v = 4/3 π•b²•c) computes the volume of an oblate spheroid based on the semi-major(b) and semi- minor (c) axis with the assumption that the spheroid is generated via rotation around the minor axis (see diagram). 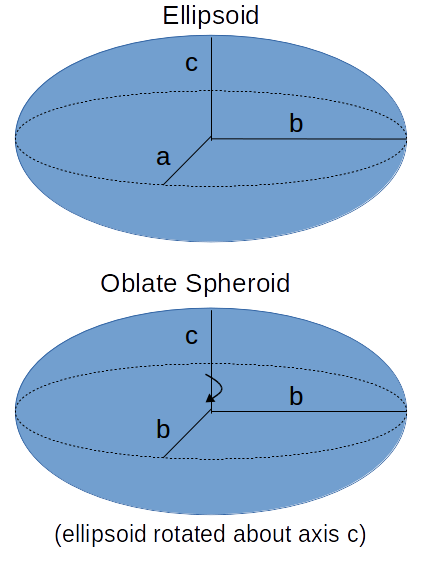
INSTRUCTIONS: Choose units and enter the following:
- (b) Semi-Major Axis (distance from oblate spheroid's center along the longest axis of spheroid)
- (c) Semi-Minor Axis (distance from oblate spheroid's center along the shortest axis of spheroid)
Oblate Spheroid Volume (V): The volume is returned in cubic meters, centimeters or kilometers. However, these can be automatically converted to other volume units (e.g. cubic yards, liters) via the pull-down menu.
The Math / Science
The formula for the volume of an oblate spheroid is:
v = 4/3 π•b²•c
where:
- V is the volume of the oblate-spheroid
- b is the length of the semi-axis rotated
- c is the length of the semi-axis of rotation
The oblate spheroid is an ellipsoid that can be formed by rotating an ellipse about its minor axis. The rotational axis thus formed will appear to be the oblate spheroid's polar axis. The oblate spheroid is fully described then by its semi-major and semi-minor axes.
One important shape in nature that is close to (though not exactly) an oblate spheroid is the Earth which has a semi-minor axis (c) which is the polar radius of 6,356 kilometers, and a semi-major axis (b) which is the equatorial radius of 6,378 kilometers. Consideration: what force would make the equatorial radius larger than the polar radius?
Ellipsoid Calculator
Ellipsoid - Volume computes the volume of an ellipsoid based on the length of the three semi-axes (a, b, c)
- Ellipsoid - Surface Area computes the surface area of an ellipsoid based on the length of the three semi-axes (a, b, c)
- Ellipsoid - Mass or Weight computes the mass or weight of an ellipsoid based on the length of the three semi-axes (a, b, c) and the mean density.
- Ellipsoid Cap - Volume computes the volume of a section of an ellipsoid.
- Oblate Spheroid - Volume computes the volume of an Oblate Spheroid based on the length of the two semi-axes (b, c)
- Oblate Spheroid- Surface Area computes the surface area of an Oblate Spheroid based on the length of the two semi-axes (b, c)
- Oblate Spheroid- Mass or Weight computes the mass or weight of an Oblate Spheroid based on the length of the two semi-axes (b, c) and the mean density.
- Sphere - Volume computes the volume of a sphere based on the length of the radius (a)
- Sphere - Surface Area computes the surface area of a sphere based on the length of the radius (a)
- Sphere - Mass or Weight computes the mass or weight of a sphere based on the length of the radius (a) and the mean density.
- Circular - Volume: Computes the volume of a column with a circular top and bottom and vertical sides.
- Circular - Mass: Computes the mass/weight of circular volume based on its dimensions and mean density.
- Elliptical Volume: Computes the volume of a column with an elliptical top and bottom and vertical sides.
- Elliptical - Mass: Computes the mass/weight of an elliptical volume based on its dimensions and mean density.
- Ellipse Vertical Chord from Edge (VE): Computes the length of the vertical chord of an ellipse based on distance from the edge.
- Ellipse Vertical Chord from Center (VC): Computes the length of the vertical chord of an ellipse based on distance from the center.
- Ellipse Horizontal Chord from Edge (HE): Computes the length of the horizontal chord of an ellipse based on distance from the edge.
- Ellipse Horizontal Chord from Center (HC): Computes the length of the vertical chord of an ellipse based on distance from the center.
- Common Mean Density: Provides a lookup function to find the mean density of hundreds of materials (woods, metals, liquids, chemicals, food items, soils, and more)
Volume is a three dimensional measurement of the amount of space taken up by an object. Volume units are cubic measurements for solid objects such as cubic inches and cubic meters. Fluids have separate volume units such as liters, fluid ounces, cups, gallons, and barrel.
The volume of an object can measured by the liquid it displaces or be calculated by measuring its dimensions and applying those dimensions to a formula describing its shape. Many such calculations are available in the following list of calculators.
In many cases, the calculators are for a column with a geometric shaped base and vertical sides. One basic formula for volume is area times a Height when the volume has vertical sides.
Volume Calculators
- Volume from Area and Height
- Volume of a Cube
- Volume of a Box
- Volume of a Cone
- Volume of a Cone Frustum
- Volume of a Cylinder
- Volume of a Slanted Cylinder
- Volume of a Semicircle
- Volume of a Triangular
- Volume of a Quadrilateral
- Volume of a Pentagon
- Volume of a Hexagon
- Volume of a Heptagon
- Volume of a Octagon
- Volume of a Nonagon
- Volume of a Decagon
- Volume of a Hendecagon
- Volume of a Dodecagon
- Volume of a Paraboloid
- Volume of a Polygon based Pyramid
- Volume of a Pyramid Frustum
- Volume of a Sphere
- Volume of a Sphere Cap
- Volume of a Sphere Segment
- Volume of a Sphere Shell
- Volume of a Oblate Spheroid
- Volume of a Ellipsoid
- Volume of a Torus
- Volume of a Bottle
- Volume of a Chamfer
- Gasket Volume
