The Volume of a Spherical Tank calculator computes the volume of a spherical tank and the amount of substance (liquid or loose granular) in the tank based on the depth of the substance and the size of the spherical container defined by its diameter and height. NOTE: NEW DEFAULT UNITS (centimeters).
INSTRUCTIONS: Choose units and enter the following:
- (d) Depth of Contents
- (D) Diameter of Spherical Tank
- (H) Height of Spherical Tank
Spherical Tank Volume (V): The calculator returns the volume of the contents (CV) and the total volume capacity of the tank (CxV) in liters. It also returns the static surface area (sA) of the contents in square meters. However, these can be automatically converted to compatible units via the pull-down menu.
Related Calculators:
- Total Volume (full) of the spherical tank
- Weight of the Load in a Spherical Tank
- Volume of a Spherical Shell.
- Mass or Weight of a Spherical Shell.
- Volume Inside of the Spherical Shell
- Volume of Torispherical Head Cylindrical Tank.
The Math / Science
The spherical tank volume formula uses the size of the tank, defined by its inner radius (R), and the depth of the contained material (D), to calculate the volume of the contained substance.CONTAINER SHAPES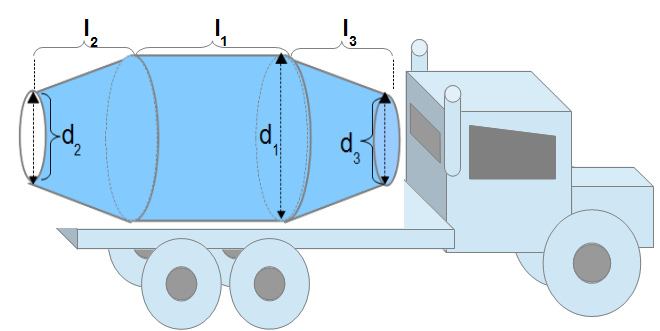
Conic Cylinder
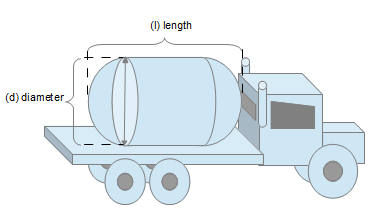Capsule Shaped
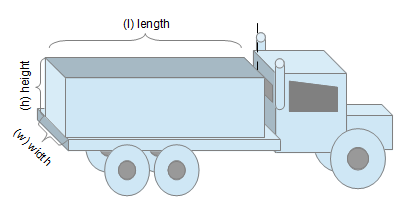Box Container 
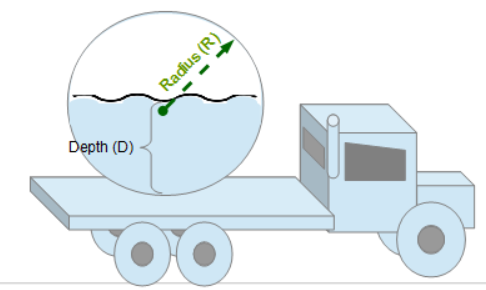Spherical Tank
Volume of a Sphere
The formula for the volume of a sphere is:
The formula for the volume of a sphere cap is:
This calculator let's the user compute the volume of a portion of the tank by subtracting the sphere cap volume from the volume of the total sphere.
Other Container Calculators
For similar calculations with other shaped containers, click on the following:
- Volume of a Conic Cylinder
- Load Weight of a Conic Cylinder
- Volume of a Capsule (Spherocylinder)
- Load Weight of a Capsule (Spherocylinder)
- Total or Partial Volume of a Box (Rectangular). For the partial volume, simply use the depth of substance in the container instead of the total depth of the container.
- Total or Partial Load Weight of a Box (Rectangular). For the weight of a partial load, simply use the depth of substance in the container instead of the total depth of the container.
- Volume of a Spherical Container
- Total or Partial Load Weight of a Spherical Container. For the total load weight, simply indicated the same value for the measure depth (D) of the substance to equal twice the radius (R) of the container. (See diagram)
- The mean density of many substances, CLICK HERE.
The Mean Density of many substances (metals, mineral, chemicals, gases, woods, agricultural products, liquids and types of earths) can be looked up by CLICKING HERE.
Or you can see these formulas and other useful measurements all combined in one TRUCKING calculator.
Plumbing Calculators
- Rolling Offsets (Run and Travel) – The Rolling Offset
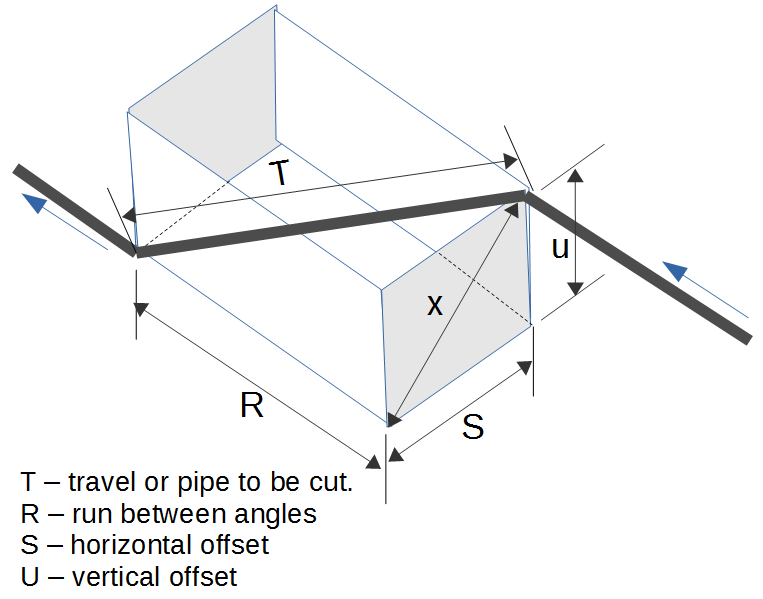Rolling Offset Lengths 
Pipe Grading function computes the run and travel length a rolling offset based on the offsets and fittings. (see diagram). - Diagonal of a Square - This is a simple calculation to assist in computing the diagonal of a square.
- Diagonal of a Box - This computes the length of the diagonal of a box (T) based on sides of length R, S and U.
- Flow Rate - This computes flow rate based on the total volume and the time it took to accumulate.
- Pipe Flow Volume - This computes the total volume from a pipe based on the flow rated and the duration of flow.
- Weight of Water in a Tank - Computes the weight of water in a cylindrical tank based on the radius and height (or length).
- Weight of Water in a Pipe - Computes the weight of water or other substances in a pipe based on the dimension and material density.
- Weight of Sea Water in pipe - Computes the weight of sea water in a cylinder based on the radius and height (or length)
- Pressure Head - The Potential Gravity-Fed Water Pressure from a Tank (a.k.a. Pressure Head) based on the height of storage.
- Pipe Volume - Computes the volume in a pipe
- Pipe Surface Area - Computes the surface area of a pipe.
- Pipe Coating Amount - Computes the volume of coating material for a pipe such as paint, polyethylene, polyurethane, zinc, bitumen, FBE or mortar.
- Pipe Grading - Compute the drop needed over a run to maintain a grade (e.g., 4" over 12')
- Volume of Water in a Tank (e.g. hot water tanks),
- Volume of a Spherical Container
- Weight of Water in a Spherical Container
- Volume of Water in Rectangular Tank
- Weight of Water in a Rectangular Tank
- Capillary Rise - The height of water in a small tube due to capillary force.
- Snow Water Equivalence - The volume of water created by an area and depth of snow.
- Pore Water Pressure - Pressure of uplift from the water table.
- Pipe Stress Budget - Computes the pressure that a pipe can withstand based on the allowable stress, wall thickness and outside diameter.