The Force Vector Component 2D calculator computes the component forces along both axes based on the magnitude of the force and the angle between the vector and the axis.
INSTRUCTIONS: Choose units and enter the following:
- |`vecF`| Magnitude of Force Vector
- (θ) Angle Away from Vector
Component Forces in 2D (Fx&y): The calculator returns the component forces in Newtons. However this can be automatically converted to compatible units via the pull-down menu.
To compute the angles from a 3D vector to the axes and the magnitude, CLICK HERE.
The Math / Science
This equation computes the component of a force in the direction of a coordinate specified in a plane (2D-Space). In a standard local coordinate system specified by orthogonal coordinates x ,y this equation expresses the component of a force `vec F` that is exerted in the direction of one of the coordinate axes.
The equations for each component are
- `vec F_x` = ` F cos(theta)`, where `theta` is the angle between the direction of the force, `vec F` and the x-axis
3D Vector Functions
 k⋅V - scalar multiplication
k⋅V - scalar multiplication- V/k - scalar division
- V / |V| - Computes the Unit Vector
- |V| - Computes the magnitude of a vector
- U + V - Vector addition
- U - V - Vector subtraction
- |U - V| - Distance between vector endpoints.
- |U + V| - Magnitude of vector sum.
- V • U - Computes the dot product of two vectors
- V x U - Computes the cross product of two vectors
- V x U • W - Computes the mixed product of three vectors
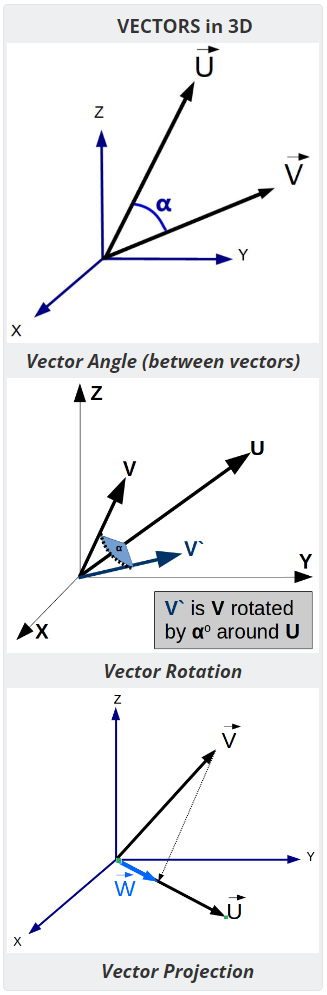
- Vector Angle - Computes the angle between two vectors
- Vector Area - Computes the area between two vectors
- Vector Projection - Compute the vector projection of V onto U.
- Vector Rotation - Compute the result vector after rotating around an axis.
- Vector Components 3D - Returns a vector's magnitude, unit vector, spherical coordinates, cylindrical coordinates and angle from each axis.
- (ρ, θ, φ) to (x,y,z) - Spherical to Cartesian coordinates
- (x,y,z) to (ρ, θ, φ) - Cartesian to Spherical coordinates
- (r, θ, z) to (x,y,z) - Cylindrical to Cartesian coordinates
- (x,y,z) to (r, θ, z) - Cartesian to Cylindrical coordinates
- (x,y) to (r, θ) - Cartesian to Polar
- (r, θ) to (x,y) - Polar to Cartesian
- Vector Normal to a Plane Defined by Three Points
