The Surface Area of Paraboloid calculator computes the surface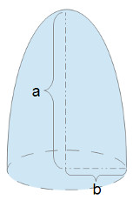
area of revolution of a parabola around an axis of length (a) of a width of (b) including the circular base.
INSTRUCTIONS: Choose units and enter the following:
- (a) Axis Length
- (b) Cross Radius
Surface Area of Paraboloid (A): The surface area is returned in square meters. However, this can be automatically converted to compatible units via the pull-down menu.
The Math / Science
The formula for the surface area of a paraboloid is:
`A = πb² + (πb) / (6a^2) * ( (b^2+4a^2)^(3/2) - b^3)`
where:
- A is the surface area of the paraboloid
- a is the length along the central axis
- b is the radius at point a
Parabola Calculators
- Parabola Formula: This computes the y coordinate of a parabola in the form y = a•x²+b•x+c
- Parabolic Area: This computes the area within a section of a parabola
- Parabolic Area (Concave): This computes the outer area of a section of a parabola.
- Parabolic Arc Length: This computes the length a long a segment of a parabola.
- Paraboloid Volume: This is the volume of a parabola rotated around an axis (i.e. paraboloid)
- Paraboloid Surface Area : This is the surface area of a paraboloid.
- Paraboloid Weight: This is the weight or mass of a paraboloid.
- Ballistic Flight Parabolic Equation: This provides the formula of the parabola that matches a ballistic flight.
Volume is a three dimensional measurement of the amount of space taken up by an object. 
Volume units are cubic measurements for solid objects such as cubic inches and cubic meters. Fluids have separate volume units such as liters, fluid ounces, cups, gallons, and barrel.
The volume of an object can measured by the liquid it displaces or be calculated by measuring its dimensions and applying those dimensions to a formula describing its shape. Many such calculations are available in the following list of calculators.
In many cases, the calculators are for a column with a geometric shaped base and vertical sides. One basic formula for volume is area times a Height when the volume has vertical sides.
Volume Calculators
- Volume of a Cube
- Volume of a Box
- Volume of a Cone
- Volume of a Cone Frustum
- Volume of a Cylinder
- Volume of a Slanted Cylinder
- Volume of a Triangular
- Volume of a Quadrilateral
- Volume of a Pentagon
- Volume of a Hexagon
- Volume of a Heptagon
- Volume of a Octagon
- Volume of a Nonagon
- Volume of a Decagon
- Volume of a Hendecagon
- Volume of a Dodecagon
- Volume of a Paraboloid
- Volume of a Polygon based Pyramid
- Volume of a Pyramid Frustum
- Volume of a Sphere
- Volume of a Sphere Cap
- Volume of a Sphere Segment
- Volume of a Sphere Shell
- Volume of a Oblate Spheroid
- Volume of a Ellipsoid
- Volume of a Torus
- Volume of a Bottle
- Volume of a Chamfer