The Parabola Calculator has formulas and 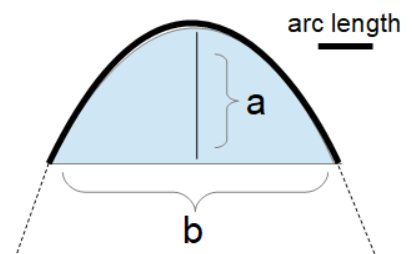     ParabolaParabola Area (Concave)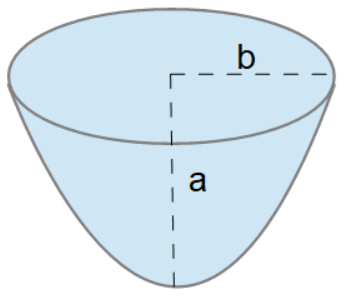Paraboloidinformation related to the parabola including:  

• Parabola Formula:  This computes the y coordinate of a parabola in the form y = a•x²+b•x+c
• Parabolic Area: This computes the area within a section of a parabola
• Parabolic Area (Concave): This computes the outer area of a section of a parabola.
• Parabolic Arc Length: This computes the length a long a segment of a parabola.
• Paraboloid Volume: This is the volume of a parabola rotated around an axis (i.e. paraboloid)
• Paraboloid Surface Area : This is the surface area of a paraboloid.
• Paraboloid Weight: This is the weight or mass of a paraboloid.
• Ballistic Flight Parabolic Equation: This provides the formula of the parabola that matches a ballistic flight.

Description of the Parabola

In mathematics, a parabola is a plane curve that is mirror-symmetrical and is approximately U-shaped. It fits several superficially different other mathematical descriptions, which can all be proved to define exactly the same curves.
Part of a parabola (blue), with various features (other colours). The complete parabola has no endpoints. In this orientation, it extends infinitely to the left, right, and upward.

One description of a parabola involves a point (the focus) and a line (the directrix). The focus does not lie on the directrix. The parabola is the locus of points in that plane that are equidistant from both the directrix and the focus. Another description of a parabola is as a conic section, created from the intersection of a right circular conical surface and a plane which is parallel to another plane that is tangential to the conical surface.

The line perpendicular to the directrix and passing through the focus (that is, the line that splits the parabola through the middle) is called the "axis of symmetry". The point on the parabola that intersects the axis of symmetry is called the "vertex", and is the point where the parabola is most sharply curved. The distance between the vertex and the focus, measured along the axis of symmetry, is the "focal length". The "latus rectum" is the chord of the parabola which is parallel to the directrix and passes through the focus. Parabolas can open up, down, left, right, or in some other arbitrary direction. Any parabola can be repositioned and rescaled to fit exactly on any other parabola—that is, all parabolas are geometrically similar. 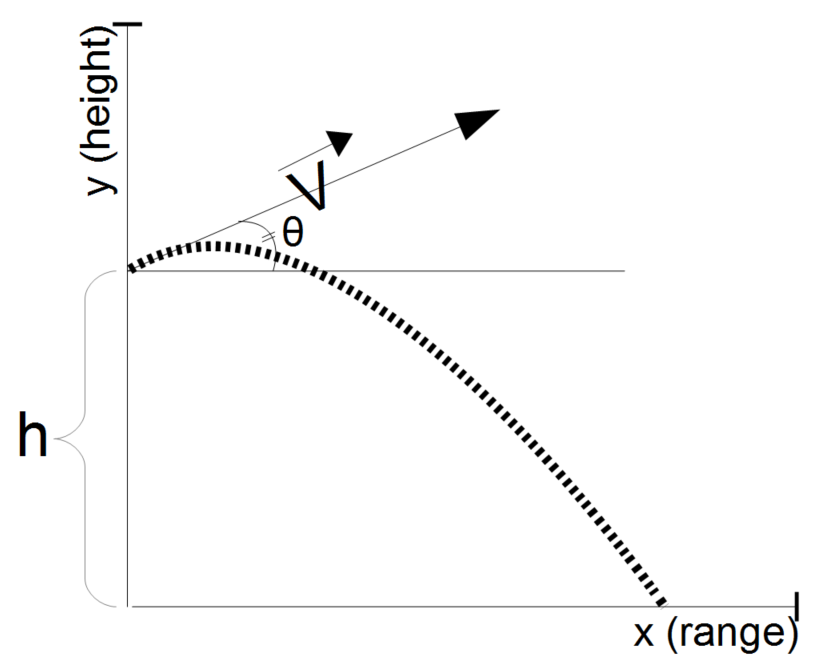Parabolic Ballistic Flight

Parabolas have the property that, if they are made of material that reflects light, then light which travels parallel to the axis of symmetry of a parabola and strikes its concave side is reflected to its focus, regardless of where on the parabola the reflection occurs. Conversely, light that originates from a point source at the focus is reflected into a parallel ("collimated") beam, leaving the parabola parallel to the axis of symmetry. The same effects occur with sound and other forms of energy. This reflective property is the basis of many practical uses of parabolas.

The parabola has many important applications, from a parabolic antenna or parabolic microphone to automobile headlight reflectors to the design of ballistic missiles. They are frequently used in physics, engineering, and many other areas. 

References

The Description of the Parabola is from Wikipedia (en.wikipedia.org/wiki/Parabola)