`L = f(a,b)`

Enter a value for all fields

The Arc Length of a Parabola calculator computes the arc length 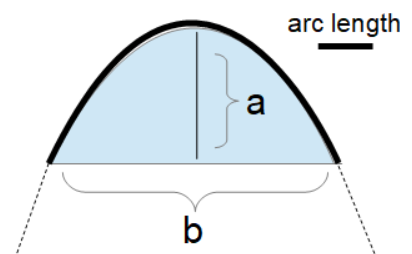of a parabola based on the distance (a) from the apex of the parabola along the axis to a point, and the width (b) of the parabola at that point perpendicular to the axis.

INSTRUCTIONS: Choose units and enter the following:

• (a)  Length Along Axis (from the apex along the axis to the chord)
• (b)  Length of Chord

Arc Length (L):  The calculator returns the length in meters.  However, this can be automatically converted to other length units via the pull-down menu.

The Math / Science

The formula for the arc length of a parabola is:

      `L = 1/2 sqrt(b^2 + 16*a^2) + b^2/(8*a) ln((4*a+sqrt(b^2+16*a^2))/b)`

where:

• L is the length of the parabola arc
• a is the length along the parabola axis
• b is the length perpendicular to the axis making a chord.

References

• “Segment of a Parabola (4.25).” Mathematical Handbook, by Murray R Spiegel, 36th ed., McGraw Hill, 1997.

---

Parabola Calculators

• Parabola Formula:  This computes the y coordinate of a parabola in the form y = a•x²+b•x+c
• Parabolic Area: This computes the area within a section of a parabola
• Parabolic Area (Concave): This computes the outer area of a section of a parabola.
• Parabolic Arc Length: This computes the length a long a segment of a parabola.
• Paraboloid Volume: This is the volume of a parabola rotated around an axis (i.e. paraboloid)
• Paraboloid Surface Area : This is the surface area of a paraboloid.
• Paraboloid Weight: This is the weight or mass of a paraboloid.
• Ballistic Flight Parabolic Equation: This provides the formula of the parabola that matches a ballistic flight.