The Boyle's Law Calculator computes the initial and final pressures and volumes based on Boyle's Law equations: P1 • V1 = P2 • V2. The calculator automatically handles numerous pressure and volume units.
P1 • V1 = P2 • V2
- (P1 = P2 • V2/V1) Initial Pressure
- (V1 = P2 • V2/P1) Initial Volume
- (P2 = P1 • V1/V2) Final Pressure
- (V2 = P1 • V1/P2) Final Volume
Boyle's law is an experimental gas law that describes how the pressure of a gas tends to decrease as the volume of a gas increases.
About Boyle's Law
Boyle’s Law states that the volume of a gas varies inversely with its pressure if temperature is held constant. Boyle's Law describes the relationship of an ideal gas where mass and temperature are kept constant. Under these conditions, the volume of the gas will vary inversely with the absolute pressure. A restatement of Boyle's Law is:
The absolute pressure exerted by a given mass of an ideal gas is inversely proportional to the volume it occupies if the temperature and amount of gas remain unchanged within a closed system.12
See main Boyle's law for further information.
Usage
Each of the four equations in this calculator are derived from the simple Boyle's Law relationship `P_1* V_1 = P_2*V_2`. Each equation assumes a fixed temperature and fixed amount of gas.
Specifically,
- Boyles Law (final pressure) computes the resultant pressure, P2 of gas resulting from a change in volume (V2 - V1) and starting pressure, P1
- Boyles Law (initial pressure) computes the initial pressure, P1 of gas prior to a change in volume (V2 - V1) with ending volume, P2
- Boyles Law (final volume) computes the resultant volume, V2 of gas resulting from a change in pressure (P2 - P1) and starting volume, V1
- Boyles Law (initial volume) computes the starting volume, V1 of gas prior to a change in pressure (P2 - P1) with ending volume, V2
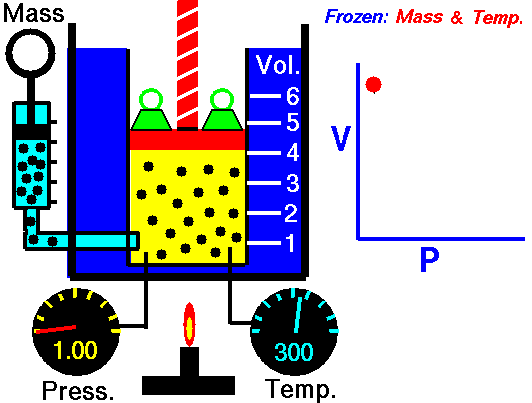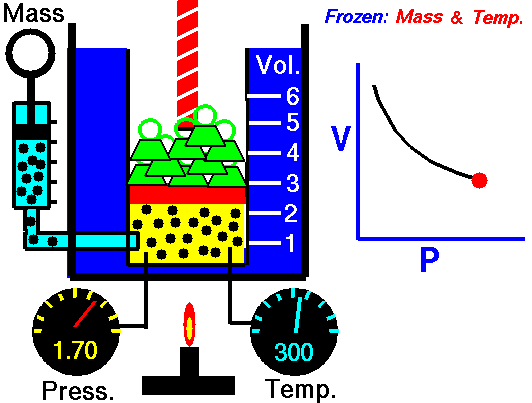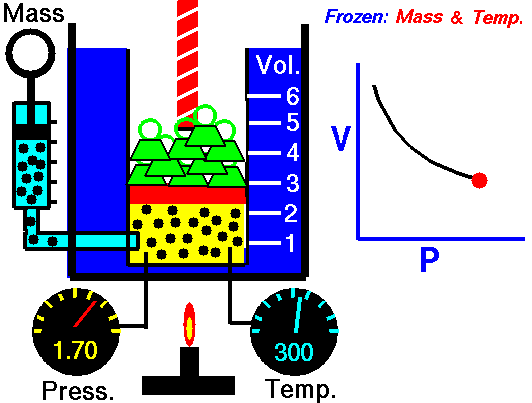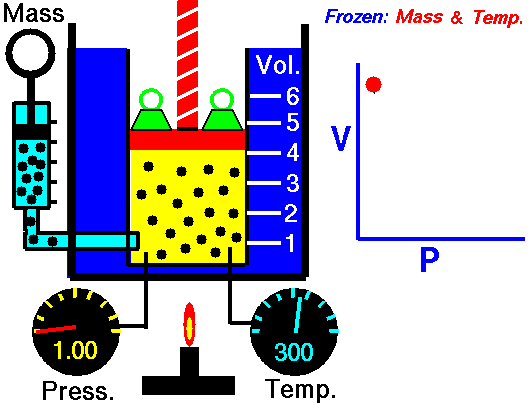 pressure is inversely proportional to volume
pressure is inversely proportional to volume
Application
This calculator may assist in many applications where pressure and volume of gas can be measured (excluding the single variable being sought) prior to and after changes in volume or pressure. However, the gas being measured must remain at a fixed amount and temperature.
Boyle's law models ideal gases. Most gases behave like ideal gases at moderate pressures and temperatures. However, as improvements in technology permitted higher pressures and lower temperatures to be examined, deviations from the ideal gas behavior were identified. It was subsequently determined that the relationship between pressure and volume can only be accurately described employing real gas theory.
Chemistry Calculators
- R - Gas Constant: 8.3144626181532 J/(K⋅mol)
- Boyle's Law Calculator: P1 • V1 = P2 • V2
- Charles Law Calculator: V1• T2 = V2 • T1
- Combined Gas Law Calculator: P•V / T= k
- Gay-Lussac Law: T1•P2 =T2•P1
- Ideal Gas Law: P•V = n•R•T
- Bragg's Law: n·λ = 2d·sinθ
- Hess' Law: ΔH0rxn=ΔH0a+ΔH0b+ΔH0c+ΔH0d
- Internal Energy: ΔU = q + ω
- Activation Energy: Ea = (R*T1⋅T2)/(T1 - T2) ⋅ ln(k1/k2)
- Arrhenius Equation: k = AeE_a/(RT)
- Clausius-Clapeyron Equation: ln(P2/P1) = (ΔHvap)/R * (1/T1 - 1/T2)
- Compressibility Factor: Z = (p*Vm)/(R*T)
- Peng-Robinson Equation of State: p = (R*T)/(Vm - b) - (a*α)/(Vm2 + 2*b*Vm - b2)
- Reduced Specific Volume: vr = v/(R* Tcr / Pc)
- Van't Hoff Equation: ΔH0 = R * ( -ln(K2/K1))/ (1/T1 - 1/T2)
