The Bragg's Law Calculator uses the Bragg's Law equation (n·λ = 2d·sinθ) to compute the distance between layers of atoms, wavelength, order of diffraction and the angle of incidence when an x-ray beam hits a crystal lattice structure.
n·λ = 2d·sinθ
Choose a button on the right to compute:
- (d) distance between layers of atoms
- (n) order of diffraction
- (λ) wavelength of x-ray
- (θ) the angle of incidence of the incoming x-ray
The default units are nanometers (nm) for wavelength and degrees for the angle of incidence, while n is a unit-less number.
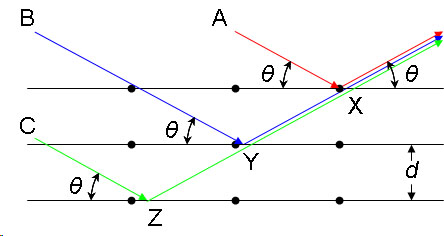
In the image below, a visual demonstration of each variable is available. Each variable "A", "B", and "C" represents an incoming x-ray beam
Image from ChemWiki (creative commons)
The Math / Science
The Bragg's Law equation, nλ = 2dsinθ, describes the relationship between different variables (described below) when an x-ray beams hits a crystal lattice structure. This formula is only used for crystal structures; if it is used for any other material, the resulting calculations are not accurate. The equation can be rearranged and used to solve for any variable in the equation. This calculator solves for n, d, θ or λ.
The parameters in Bragg's Law are:
- (d) distance between layers of atoms
- (n) order of diffraction
- (λ) wavelength of x-ray
- (θ) the angle of incidence of the incoming x-ray
The Bragg's Law equation is used in chemistry to help describe the scattering effects when an x-ray is shone onto a crystal lattice, and is often used for X-Ray Diffraction (XRD). If the crystal structure is known, then Bragg's Law can be used to calculate the wavelength of the x-rays hitting its surface. However, if the crystal structure is unknown, then the incoming x-ray information can be used to calculate details about the crystal lattice structure. This information is useful to chemists and can provide data on new crystal lattice structures.
Chemistry Calculators
- R - Gas Constant: 8.3144626181532 J/(K⋅mol)
- Boyle's Law Calculator: P1 • V1 = P2 • V2
- Charles Law Calculator: V1• T2 = V2 • T1
- Combined Gas Law Calculator: P•V / T= k
- Gay-Lussac Law: T1•P2 =T2•P1
- Ideal Gas Law: P•V = n•R•T
- Bragg's Law: n·λ = 2d·sinθ
- Hess' Law: ΔH0rxn=ΔH0a+ΔH0b+ΔH0c+ΔH0d
- Internal Energy: ΔU = q + ω
- Activation Energy: Ea = (R*T1⋅T2)/(T1 - T2) ⋅ ln(k1/k2)
- Arrhenius Equation: k = AeE_a/(RT)
- Clausius-Clapeyron Equation: ln(P2/P1) = (ΔHvap)/R * (1/T1 - 1/T2)
- Compressibility Factor: Z = (p*Vm)/(R*T)
- Peng-Robinson Equation of State: p = (R*T)/(Vm - b) - (a*α)/(Vm2 + 2*b*Vm - b2)
- Reduced Specific Volume: vr = v/(R* Tcr / Pc)
- Van't Hoff Equation: ΔH0 = R * ( -ln(K2/K1))/ (1/T1 - 1/T2)
Supplemental Material
Bragg's Law: solving for wavelength (λ)
References
Whitten, et al. "Chemistry" 10th Edition. Pp. 476