`A = 2*pi* "h" * sqrt(( [ ( r_1 - r_2 )^2 + "h" ^2] * [ ( r_1 + r_2 )^2+ h^2])/(4*h^2)) + pi * (r_1^2 + r_2^2)`

Enter a value for all fields

The Surface Area of a Sphere Segment calculator computes the surface area of a slice of a sphere made by two parallel plane cutting through the sphere (See Diagram)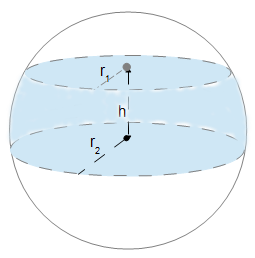 including the top and bottom circles. 

INSTRUCTIONS: Choose units and enter the following:

• (r₁) upper radius
• (r₂) lower radius
• (h) distance between the parallel planes. (See diagram)  

Sphere Frustum Surface Area (A): The surface area is returned in square meters.  However, this can be automatically converted to compatible units via the pull-down menu.

The Math / Science

The Total Surface Area of a Sphere Segment formula is:

`A = 2pih * sqrt(( [ (r_1-r_2)^2 + h^2] * [ (r_1+r_2)^2+ h^2])/(4*h^2)) + pi(r_1^2+r_2^2)`

where:

• A = Surface Area of Sphere Frustum including top and bottom circles
• r₁ = top radius
• r₂ = bottom radius
• h = distance between planes

This formula computes the surface area of a slice of a sphere made by two parallel plane cutting through the sphere (See Diagram) .  A sphere slice could be considered a sphere frustum.  The assumption is that both slices are in parallel planes. (See diagram)  The surface area includes the top and bottom circles created by the two planes slicing through the sphere.

Uses

Many manufactured objects are in the shape of a a sphere segment (aka sphere slice or sphere frustum).  This formula can also be used to approximate the surface area of an apple, in essence the area of the apple skin.

---

Sphere Calculators

• Sphere Surface Area based radius (r)
• Sphere Surface Area from Volume
• Sphere Volume from Radius
• Sphere Volume from Circumference
• Sphere Volume from Surface Area
• Sphere Volume from Mass and Density
• Sphere Radius from Volume
• Sphere Radius from Surface Area
• Sphere Weight (Mass) from volume and density
• Sphere Density
• Area of Triangle on a Sphere
• Distance between Two Points on a Sphere
• Sphere Cap Surface Area
• Sphere Cap Volume
• Sphere Cap Weight (Mass) 
• Sphere Segment Volume
• Sphere Segment Weight (Mass)
• Sphere Segment Wall Surface Area (without the circular top and bottom ends)
• Sphere Segment Full Surface Area  (with the top and bottom circles, aka ends)
• Volume of Spherical Shell
• Mass of Spherical Shell