The Capillary Rise calculator equation computes the height of liquid in a small diameter tube due to capillary force on the liquid. 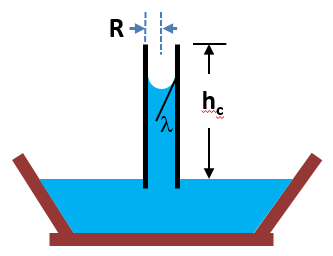
INSTRUCTIONS: Choose units and enter the following:
- (σ) Surface Tension of Fluid (Default: Surface Tension of Water at STP)
- (λ) Meniscus Angle
- (ρw) Density of Fluid (Default: Density of Water at STP)
- (R) Radius of Capillary Tube
Capillary Rise (hc): The calculator returns the rise in millimeters. However this can be automatically converted into other length units via the pull-down menu.
The Math / Science
The formula for the capillary rise is: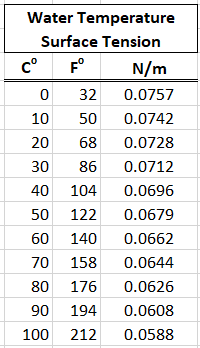
where:
- hc is the capillary rise
- σ is the surface tension
- λ is the meniscus angle
- ρ is the density
- R is the radius of the tube
The force on the fluid is caused by the attraction between the solid and the liquid which pulls the water up into the tube. The water rises until the force of capillary attraction is offset by the force due to gravity on the water column. The surface of the water in the tube meets the walls of the tube at a contact angle that is unique to the fluid, in this case water, creating a concave upper surface to the water. The rise of the water is computed from the following:
surface tension of the water
- angle of the meniscus, the angle at which the water surface intersects the sides of the tube
- density of the fluid
- local acceleration due to gravity (assumed at sea level)
- the radius of the tube
| Type of snow or ice | (kg/m3) |
| Fresh New snow | 50-70 |
| Damp new snow | 100-200 |
| Settled snow | 200-300 |
| Depth hoar | 100-300 |
| Wind packed snow | 350-400 |
| Firn (granular) | 400-830 |
| Very wet | 700-800 |
| Glacier ice | 830-917 |
| Rain/Melt | 997 |
Hydrology (Water, Rain and Snow) Calculators:
- Snow Pack to Liquid Water Calculator
- Volume of water in snow or rain
- Weight/Mass of Snow on an Area.
- Weight of Snow on a Rectangular Area.
- Weight of Snow on a Roof.
- Weight of Snow on a Polygon Shaped Area.
- Volume of Water in a Rainfall
- Flow Rate of Broad Crested Weir
- Water Capillary Rise.
- Volume of Flood Water.
- Number of sandbags needed to build a wall or dike.
- Water Saturation Ratio
- Rain Fall Harvesting Calculator
- Peak Discharge from Drainage Basin Runoff
- Gauckler-Manning Equation
- Cipolletti Weir Flow Rate
- Acre-feet
Plumbing Calculators
- Rolling Offsets (Run and Travel) – The Rolling Offset
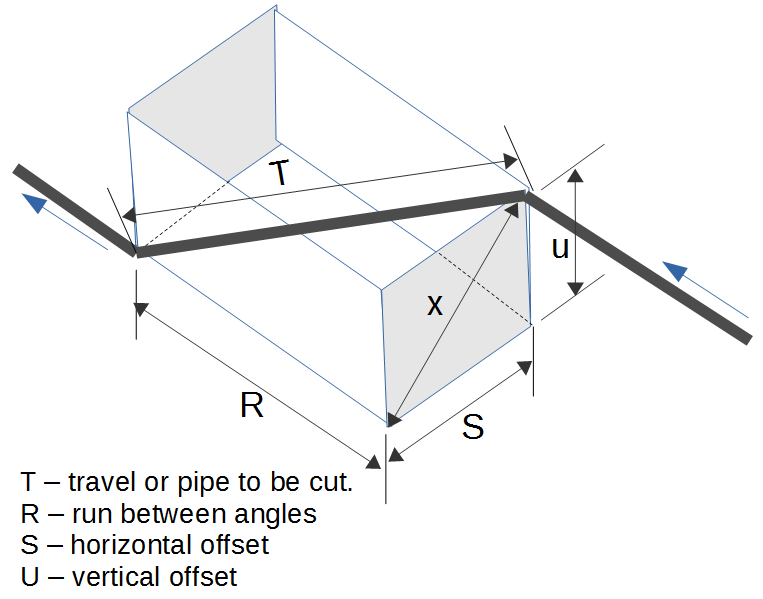 Rolling Offset Lengths
Rolling Offset Lengths Pipe Grading function computes the run and travel length a rolling offset based on the offsets and fittings. (see diagram).
- Pipe Grading - Compute the drop needed over a run to maintain a grade (e.g., 4" over 12')
- Diagonal of a Square - This is a simple calculation to assist in computing the diagonal of a square.
- Diagonal of a Box - This computes the length of the diagonal of a box (T) based on sides of length R, S and U.
- Flow Rate - This computes flow rate based on the total volume and the time it took to accumulate.
- Pipe Flow Volume - This computes the total volume from a pipe based on the flow rated and the duration of flow.
- Weight of Water in a Tank
- Computes the weight of water in a cylindrical tank based on the radius and height (or length).
- Weight of Water in a Pipe - Computes the weight of water or other substances in a pipe based on the dimension and material density.
- Weight of Sea Water in pipe - Computes the weight of sea water in a cylinder based on the radius and height (or length)
- Pressure Head - The Potential Gravity-Fed Water Pressure from a Tank (a.k.a. Pressure Head) based on the height of storage.
- Pipe Volume - Computes the volume in a pipe.
- Pipe Surface Area - Computes the surface area of a pipe.
- Pipe Coating Amount - Computes the volume of coating material for a pipe such as paint, polyethylene, polyurethane, zinc, bitumen, FBE or mortar.
- Volume of Water in a Tank (e.g. hot water tanks),
- Volume of a Spherical Container
- Weight of Water in a Spherical Container
- Volume of Water in Rectangular Tank
- Weight of Water in a Rectangular Tank
- Capillary Rise - The height of water in a small tube due to capillary force.
- Snow Water Equivalence - The volume of water created by an area and depth of snow.
- Pore Water Pressure - Pressure of uplift from the water table.
- Pipe Stress Budget - Computes the pressure that a pipe can withstand based on the allowable stress, wall thickness and outside diameter.
- Water in Basement Volume: Computes the volume of water in an area such as a basement based on the dimensions and the time required to pump it out based on a sump pump rate.
- Paint for Pipes: Computes the amount of paint needed to cover the exterior surface area of one or more pipes based on the pipe diameter, length, number of coats, number of pipes and the recommended area coverage of the paint.
- Time to Fill: Computes the amount of time necessary to fill something (e.g., tank or pool) based on the volume and flow rate.
- Pipe Insulation Calc: Computes the number of bags of pipe insulation needed for a run of pipes based on the 12' of length per bag and the length of pipe run to be insulated.
- Head Height: Computes the head height of liquid needed to achieve a pressure for a liquid (default is water).
