The Eccentricity of an Ellipse calculator computes the eccentricity of a conic section (e.g., ellipse) based on the lengths of the semi major and minor axes. 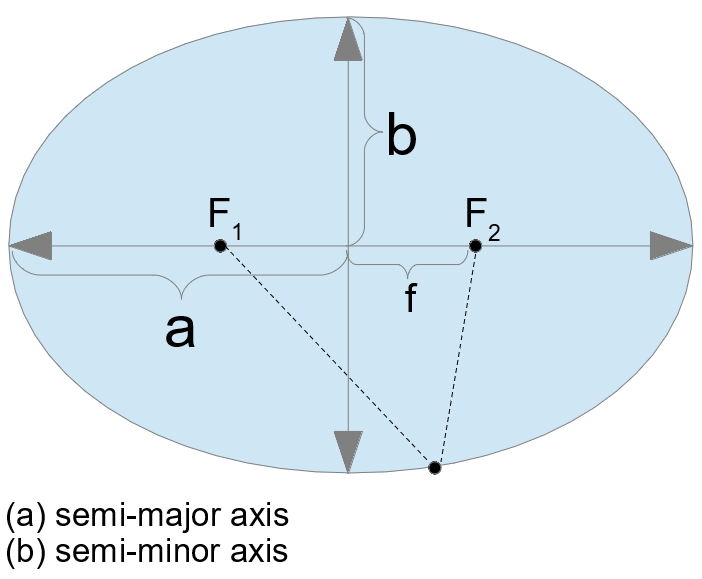
INSTRUCTIONS: Choose units and enter the following:
- (a) semi-major axis (see diagram)
- (b) semi-minor axis (see diagram)
Eccentricity (e): The calculator returns the eccentricity of the ellipse.
The Math / Science
In mathematics, an ellipse is a curve in a plane surrounding two focal points such that the sum of the distances to the two focal points is constant for every point on the curve. As such, it is a generalization of a circle, which is a special type of an ellipse having both focal points at the same location. The shape of an ellipse (how "elongated" it is) is represented by its eccentricity, which for an ellipse can be any number from 0 (the limiting case of a circle to arbitrarily close to but less than 1.
The formula for the eccentricity of an ellipse is:
`e = sqrt(1 - (b^2/a^2))`
where:
- e = eccentricity
- a = length of the semi-major axis
- b = length of the semi-minor axis
Eccentricity and Conic Sections
- The eccentricity of a circle is zero, where a = b
- The eccentricity of an ellipse is from zero up to, but not including 1.
- The eccentricity of a parabola is 1.
- The eccentricity of a hyperbola is greater than one.
Ellipse Calculators
An ellipse is defined by the semi-major axis (A) and semi-minor axis (B).
- Area of Ellipse: Computes the area of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
- Rumanujan's Circumference of an Ellipse 1 : The first of two of Rumanujan's approximations of the circumference (perimeter) of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
- Rumanujan's Circumference of an Ellipse 2: The second Rumanujan approximations of the circumference (perimeter) of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
- Circumference of an Ellipse (other) Another common estimation of the circumference (perimeter) of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
- Ellipse Axis Length: Approximates one axis of an ellipse bases on the circumference and the other axis.
- Eccentricity of an Ellipse
Computes the eccentricity of an ellipse which is based on the ratios of the semi-major axis (a) and the semi-minor axis (b).
- Linear Eccentricity of an Ellipse (f) Computes the distance from the center to either foci (f), which is the linear eccentricity of an ellipse. This is based on the semi-major axis (a) and the semi-minor axis (b).
- Mean Radius of an Ellipse Computes the mean radius of an ellipse. This would define a circle with the same approximate area, based on the ellipse's semi-major axis (a) and the semi-minor axis (b).
- Elliptical Volume Computes the volume of a column with an elliptical base.
Ellipse Chords
- Ellipse Vertical Chord from Edge (VE): Computes the length of the vertical chord of an ellipse based on distance from the edge.
- Ellipse Vertical Chord from Center (VC): Computes the length of the vertical chord of an ellipse based on distance from the center.
- Ellipse Horizontal Chord from Edge (HE): Computes the length of the horizontal chord of an ellipse based on distance from the edge.
- Ellipse Horizontal Chord from Center (HC): Computes the length of the vertical chord of an ellipse based on distance from the center.
Ellipsoid (3D Elliptical Shape)
- Ellipsoid - Volume computes the volume of an ellipsoid based on the length of the three semi-axes (a, b, c)
- Ellipsoid - Surface Area computes the surface area of an ellipsoid based on the length of the three semi-axes (a, b, c)
- Ellipsoid - Mass or Weight computes the mass or weight of an ellipsoid based on the length of the three semi-axes (a, b, c) and the mean density.
.
