The Nuclear Binding Energy calculator computes the energy released in the formation of an atom based on the change in mass (Δm).
INSTRUCTIONS: Choose units and enter the following:
Nuclear Binding Energy (E): The calculator returns the energy in Mega-electron volts (MeV). However, this can be automatically converted to compatible units (e.g. Joules) via the pull-down menu.
Note: This calculator has been updated. The default input units have been changed from grams (g) to atomic mass units (u) and output units from Joules (J) to Mega electron volts (MeV). Grams and Joules are still available via the pull-down menu. Also, the speed of light squared is now used in units of MeV/u .
The Math / Science
The equation for Nuclear Binding Energy calculates the energy released in the formation of an atom from subatomic particles. This can be expressed in a rewritten form of the Einstein relationship:
E = Δm⋅c2
Where:
- E = nuclear binding energy
- Δm = difference in mass of the alpha particle and the sum of its parts (protons and neutrons)
- c2 = speed of light squared (931.46 MeV/u)
Nuclear binding energy is the energy equivalent of the mass deficiency of an atom. Mass deficiency is the amount of matter that would be converted into energy if an atom were constructed from fundamental particles1. So, essentially, nuclear binding energy is the energy released from an atom if it were formed from individual protons and neutrons.
Nuclear Fusion
In the most common fusion experiments, Deuterium and Tritium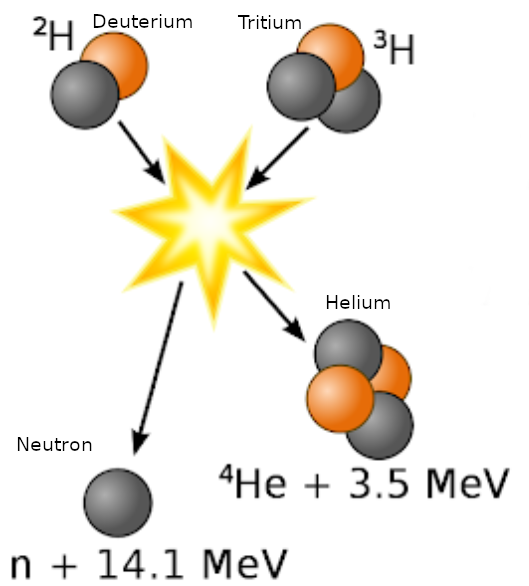 
are super heated in devices like a tokamak at ITER to cause a fusion reaction (see graphic). This is known as a DT reaction. In a DT reaction, the Deuterium and Tritium are fused together and create a Helium 4 atom with an energy state of 3.5 MeV, and a highly energetic neutron at 14.1 MeV. The following lists their mass in atomic mass units (u):
- Deuterium (2H): 2.01410177811 u
- Tritium (3H) : 3.016049281 u
to
- Helium (4He): 4.00260325413 u
- Neutron: 1.0086649158 u
The delta in mass is `Delta_m `= 0.0188828 u. If you use the binding energy formula in this calculator, the released energy equivalent to 0.0188828 u is equal to 17.588 MeV, which is the sum of the 14.1 MeV neutron and the 3.5 MeV Helium atom in the graphic above.
Dedication
This calculator is dedicated to the scientists and administrators at the U.S. Department of Energy in the Office of Science (Fusion Energy Sciences) and in ARPA-E. These scientists have kept the dream of abundant energy through nuclear fusion alive. Thanks to their hard work, the world is rapidly approaching the miracle of capturing the power of the Sun here on Earth. Nuclear fusion creates astonishing amounts of energy using abundantly available materials (sea water and lithium). Nuclear fusion creates no greenhouse gasses and poses no long-term radioactive waist. Commercially viable nuclear fusion reactors will change the world. See The Nuclear Energy we all need and want, NUCLEAR FUSION.
Mass and Matter Information
- Force of Gravity
- Mass of an Electron
- Mass of a Proton
- Mass of a Neutron
- Atomic Mass Deficiency - Difference between atom components (protons, neutrons and electrons) and the mass of the atom.
Energy Calculators
- Kinetic Energy: `KE= 1/2 *m * v^2`
- Kinetic Energy (change of velocity): `KE = 1/2*m*(V_1-V_2)^2`
- Relativistic Kinetic Energy: `E_K = (m*c^2)/sqrt(1 - v^2"/"c^2") - m*c^2`
- Potential Energy: `U(y) = m*g*y`
- Potential Energy of Gravity (two bodies): `U(G) = - (G*m1*m2)/r`
- Nuclear Binding Energy: `E = m*c^2`
- Quantum Energy (Planck's Equation): `E = h*f`
- Energy of a Particle in a Box: `E_n=(n^2h^2)/(8mL^2)`
- Molecular Kinetic Energy: `KE = 3/2 * k_B *T`
- Electrostatic Potential Energy: `E_(el) = k_e * (Q_1*Q_2)/d`
- Photon Energy from Wavelength: `E = (h*c)/lambda`
- Heat Energy to Change Material Temperature: `Q = C * m *DeltaT`
Supplemental Material
HyperPhysics: Nuclear Binding Energy
Chem.Purdue: Nuclear Binding Energy
References
[1] Whitten, et al. "Chemistry" 10th Edition. Pp. 855-856