22.3 The electric field by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
22.3 The electric field
The definition of the electric field is directly analogous to, and has the same motivation as, the definition of the gravitational field.
definition of the electric field: The electric field vector, E, at any location in space is found by placing a test charge qt at that point. The electric field vector is then given by formula
where F is the electric force on the test charge.
Charges are what create electric fields. Unlike gravity, which is always attractive, electricity displays both attraction and repulsion. A positive charge is a source of electric fields, and a negative one is a sink.
The most difficult point about the definition of the electric field is that the force on a negative charge is in the opposite direction compared to the field. This follows from the definition, since dividing a vector by a negative number reverses its direction. It's as though we had some objects that fell upward instead of down.
self-check:
Find an equation for the magnitude of the field of a single point charge Q.
Example 3: Superposition of electric fields
⇒ Charges q and -q are at a distance b from each other, as shown in the figure. What is the electric field at the point P, which lies at a third corner of the square?
⇒ The field at P is the vector sum of the fields that would have been created by the two charges independently. Let positive x be to the right and let positive y be up.
Negative charges have fields that point at them, so the charge -q makes a field that points to the right, i.e., has a positive x component. Using the answer to the self-check, we have
`E_(-q,x)=k_q/b^2`
`E_(-q,y)=0.`
Note that if we had blindly ignored the absolute value signs and plugged in -q to the equation, we would have incorrectly concluded that the field went to the left.
By the Pythagorean theorem, the positive charge is at a distance `sqrt(2)b` from P, so the magnitude of its contribution to the field is `E=(kq)/(2b^2)`. Positive charges have fields that point away from them, so the field vector is at an angle of 135° counterclockwise from the x axis.
`E_(q,x)=(kq)/(2b^2)cos 135°`
`=-(kq)/(2^(3"/"2)b^2`
`E_(q,y)=(kq)/(2b^2)sin 135°`
`=(kq)/(2^(3/2)b^2)`
The total field is
`E_x=(1-2^(-3/2))(kq)/(b^2)`
`E_y=(kq)/(2^(3/2)b^2)`.
Example 4: A line of charge
In a complete circuit, there is typically no net charge on any of the wires. However, there are some devices in which a circuit is intentionally left open in order to produce a nonzero net charge on a wire. One example is a type of radiation detector called a Geiger-Müller tube, figure j. A high voltage is applied between the outside of the cylinder and the wire that runs along the central axis. A net positive charge builds up on the wire and a negative one on the cylinder's wall. Electric fields originate from the wire, spread outward from the axis, and terminate on the wall. The cylinder is filled with a low-pressure inert gas. An incoming particle of radioactivity strikes an atom of the gas, ionizing it, i.e., splitting it into positively and negatively charged parts, known as ions. These ions then accelerate in opposite directions, since the force exerted by an electric field on a charged particle flips directions when the charge is reversed. The ions accelerate up to speeds at which they are capable of ionizing other atoms when they collide with them. The result is an electrical avalanche that causes a disturbance on the voltmeter.
Motivated by this example, we would like to find how the field of a long, uniformly charged wire varies with distance. In figure k/1, the point P experiences a field that is the vector sum of contributions such as the one coming from the segment q. The field Eq arising from this segment has to be added to similar contributions from all other segments of the wire. By symmetry, the total field will end up pointing at a right angle to the wire. We now consider point P', figure k/2, at twice the distance from the wire. If we reproduce all the angles from k/1, then the new triangle is simply a copy of the old one that has been scaled up by a factor of two. The left side's length has doubled, so `q'=2q`, and this would tend to make Eq' twice as big. But all the distances have also been doubled, and the 1/r2 in Coulomb's law therefore contributes an additional factor of 1/4. Combining these two factors, we find `E_q'=E_q/2`. The total field is the sum of contributions such as Eq', so if all of these have been weakened by a factor of two, the same must apply to the total as well. There was nothing special about the number 2, so we conclude that in general the electric field of a line of charge is proportional to 1/r.
Applying this to the Geiger-Müller tube, we can see the reason why the device is built with a wire. When r is small, 1/r is big, and the field is very strong. Therefore the device can be sensitive enough to trigger an avalanche in the gas when only a single atom has been ionized.
We have only shown that the field is proportional to 1/r, but we haven't filled in the other factors in the equation. This is done in example 14 on p. 639.
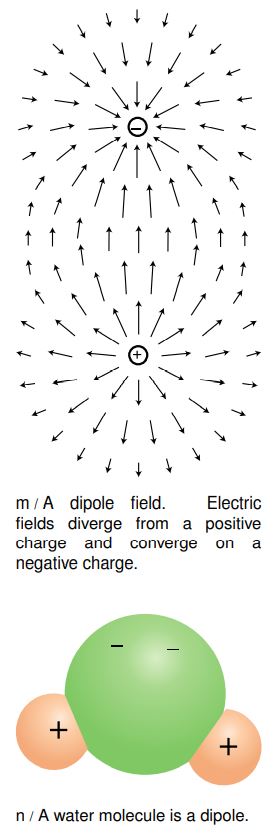Dipoles
Your microwave oven acts on water molecules with electric fields. Let us imagine what happens if we start with a uniform electric field, l/1, made by some external charges, and then insert a dipole, l/2, consisting of two charges connected by a rigid rod. The dipole disturbs the field pattern, but more important for our present purposes is that it experiences a torque. In this example, the positive charge feels an upward force, but the negative charge is pulled down. The result is that the dipole wants to align itself with the field, l/3. The microwave oven heats food with electrical (and magnetic) waves. The alternation of the torque causes the molecules to wiggle and increase the amount of random motion. The slightly vague definition of a dipole given above can be improved by saying that a dipole is any object that experiences a torque in an electric field.
`τ =(L/2)*q*|E|*sinθ+(L/2)*q*|E|*sinθ`
(Note that even though the two forces are in opposite directions, the torques do not cancel, because they are both trying to twist the dipole in the same direction.) The quantity L⋅q is called the dipole moment, notated D. (More complex dipoles can also be assigned a dipole moment --- they are defined as having the same dipole moment as the two-charge dipole that would experience the same torque.)
Example 5: Dipole moment of a molecule of NaCl gas
⇒ In a molecule of NaCl gas, the center-to-center distance between the two atoms is about 0.6 nm. Assuming that the chlorine completely steals one of the sodium's electrons, compute the magnitude of this molecule's dipole moment.
⇒ The total charge is zero, so it doesn't matter where we choose the origin of our coordinate system. For convenience, let's choose it to be at one of the atoms, so that the charge on that atom doesn't contribute to the dipole moment. The magnitude of the dipole moment is then
D=(6×10-10 m)(e)
=(6×10-10 m)(1.6×10-19 C)
=1×10-28 C⋅m
Alternative definition of the electric field
alternative definition of the electric field: The electric field vector, E, at any location in space is defined by observing the torque exerted on a test dipole Dt placed there. The direction of the field is the direction in which the field tends to align a dipole (from - to +), and the field's magnitude is |E|=τ/Dtsinθ
The main reason for introducing a second definition for the same concept is that the magnetic field is most easily defined using a similar approach.
Voltage related to electric field
`DeltaPE=-Fd`,[assuming constant force and motion parallel to the force]
and divide by charge,
`(DeltaPE)/q=(-F/q)d,`
giving
In other words, the difference in voltage between two points equals the electric field strength multiplied by the distance between them. The interpretation is that a strong electric field is a region of space where the voltage is rapidly changing. By analogy, a steep hillside is a place on the map where the altitude is rapidly changing.
Example 6: Field generated by an electric eel
⇒ Suppose an electric eel is 1 m long, and generates a voltage difference of 1000 volts between its head and tail. What is the electric field in the water around it?
⇒ We are only calculating the amount of field, not its direction, so we ignore positive and negative signs. Subject to the possibly inaccurate assumption of a constant field parallel to the eel's body, we have
`|E|=(DeltaV)/(Deltax)=1000 V"/"m.`
Example 7: The hammerhead shark
One of the reasons hammerhead sharks have their heads shaped the way they do is that, like quite a few other fish, they can sense electric fields as a way of finding prey, which may for example be hidden in the sand. From the equation |E|= ΔV)/ Δx, we can see that if the shark is sensing the voltage difference between two points, it will be able to detect smaller electric fields if those two points are farther apart. The shark has a network of sensory organs, called the ampullae of Lorenzini, on the skin of its head. Since the network is spread over a wider head, the Δx is larger. Some sharks can detect electric fields as weak as 50 picovolts per meter!
Example 8: Relating the units of electric field and voltage
From our original definition of the electric field, we expect it to have units of newtons per coulomb, N/C. The example above, however, came out in volts per meter, V/m. Are these inconsistent? Let's reassure ourselves that this all works. In this kind of situation, the best strategy is usually to simplify the more complex units so that they involve only mks units and coulombs. Since voltage is defined as electrical energy per unit charge, it has units of J/C:
`V/m=(J"/"C)/m=J/(C*m).`
To connect joules to newtons, we recall that work equals force times distance, so J=N⋅m, so
`V/m=(N*m)/(C*m)=N/C`
As with other such difficulties with electrical units, one quickly begins to recognize frequently occurring combinations.
Discussion Questions
A - In the definition of the electric field, does the test charge need to be 1 coulomb? Does it need to be positive
B - Does a charged particle such as an electron or proton feel a force from its own electric field?
C - Is there an electric field surrounding a wall socket that has nothing plugged into it, or a battery that is just sitting on a table?
D - In a flashlight powered by a battery, which way do the electric fields point? What would the fields be like inside the wires? Inside the filament of the bulb?
E - Criticize the following statement: “An electric field can be represented by a sea of arrows showing how current is flowing.”
F - The field of a point charge, |E|=kQ/r2, was derived in the self-check above. How would the field pattern of a uniformly charged sphere compare with the field of a point charge?
G - The interior of a perfect electrical conductor in equilibrium must have zero electric field, since otherwise the free charges within it would be drifting in response to the field, and it would not be in equilibrium. What about the field right at the surface of a perfect conductor? Consider the possibility of a field perpendicular to the surface or parallel to it.
H - Compare the dipole moments of the molecules and molecular ions shown in the figure.
I - Small pieces of paper that have not been electrically prepared in any way can be picked up with a charged object such as a charged piece of tape. In our new terminology, we could describe the tape's charge as inducing a dipole moment in the paper. Can a similar technique be used to induce not just a dipole moment but a charge?
J - The earth and moon are fairly uneven in size and far apart, like a baseball and a ping-pong ball held in your outstretched arms. Imagine instead a planetary system with the character of a double planet: two planets of equal size, close together. Sketch a sea of arrows diagram of their gravitational field.
22.3 The electric field by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.