The Perimeter of a Polygon (Outer Radius) calculator computes the length of the perimeter of a regular polygon of (n) sides that is circumscribed by an outer circle of radius (r).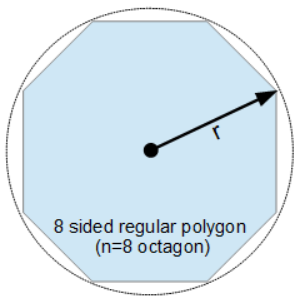
INSTRUCTIONS: Choose units and enter the following:
- (n) Number of Sides in the regular polygon.
- (r) Radius of Circle containing the polygon where the corners of the polygon are all on the circle.
Polygon Perimeter (P): The calculator return to total perimeter of the regular polygon in meters. However this can be automatically converted to compatible units via the pull-down menu.
The Math / Science
A regular n-sided polygon is a polygon with n equal length sides and is a polygon which has n equal angles at the n vertices of the polygon. Because of the symmetry of this construction, all the vertices of the regular polygon lie on the circle and the sides of the regular polygons form n chords of the circle. The formula for the perimeter of a polygon based on the number of sides and the outer radius is:
P = 2⋅n⋅r⋅sin(π/n)
where:
- P is the perimeter of the polygon
- n is the number of sides
- r is the outer radius of the polygon
Regular Polygon Information
A regular polygon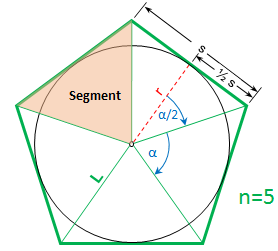
is a geometric shape with three or more straight sides where every side is the same length and every angle between connecting sides are the same angle. Because of the symmetry of the regular polygon, all the vertices of the polygon can be constructed to touch a circle in which the regular polygon is inscribed and all the chords that are polygon sides will then obviously be of equal length . Likewise, because of the regular polygon's symmetry, a circle constructed to be inscribed in a regular polygon and touching the polygon will touch the regular polygon at the midpoint of the polygon side. As shown in the pictures, Figure 1 and Figure 2, lines from the regular polygon's vertices to the circle's center form n isosceles triangles of equal area.
The names of polygons vary based on the number of sides as follows:
- triangle - 3 sides
- square - 4 sides
- pentagon - 5 sides
- hexagon - 6 sides
- heptagon - 7 sides
- octagon - 8 sides
- nonagon - 9 sides
- decagon - 10 sides
- hendecagon - 11 sides
- dodecagon - 12 sides
Common Regular Polygon Functions
Polygon Area Calculators:
- Polygon Area from the Number of sides and Length of Sides
- Polygon Area from the Number of Sides and Outside Radius
- Area of a Polygon Segment (triangle) from the Number of Sides and Inscribed Radius
- Polygon Area from the Number of Sides and Inscribed Radius.
Polygon Side Calculators
- Length of a Polygon Side from the Number of Sides and Outer Radius
- Length of a Polygon Side from the Number of Sides and Inner Radius
Polygon Perimeter Calculators
- Perimeter of a Polygon from Number of Sides and Length of Sides
- Perimeter of a Polygon from Number of Sides and Outer Radius
- Perimeter of a Polygon from Number of Sides and Inner Radius
3D Polygon Shapes
Other Polygon Calculators
- Interior Angle of a Regular Polygon based on the number of sides
- Area of Circle - Circle approximates a polygon as the number of sides approaches infinity.
- Area of Triangle - Three Sides
- Area of a Square - Four Sides
- Area of Pentagon - Five Sides
- Area of Hexagon - Six Sides
- Area of Heptagon - Seven Sides
- Area of Octagon - Eight Sides
- Area of Nonagon - Nine Sides
- Area of Decagon - Ten Sides
- Area of Hendecagon - Eleven Sides
- Area of Dodecagon - Twelve Sides