This Area of a Polygon (Outer Radius) calculator computes the area of a regular polygon with (n) equal sides inside of an outer radius (r).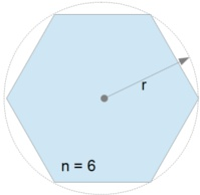 
INSTRUCTIONS: Choose units and enter the following:
- (n) Number of Sides
- (r) Outer Radius of Polygon
Total Area (A): The area returned in square meters. However, this can be automatically converted to other area units via the pull-down menu.
The Math / Science
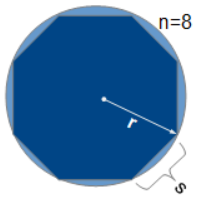The formula for the area of a polygon based on the number of sides and outer radius is:
A = ½• n • r² • sin( (2π) / n)
where:
- A is the area of a polygon
- r is the outer radius
- n is the number of sides
Regular Polygon Information
A regular polygon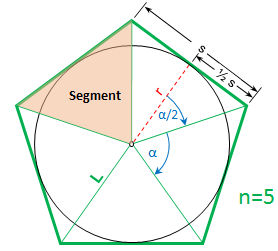
is a geometric shape with three or more straight sides where every side is the same length and every angle between connecting sides are the same angle. Because of the symmetry of the regular polygon, all the vertices of the polygon can be constructed to touch a circle in which the regular polygon is inscribed and all the chords that are polygon sides will then obviously be of equal length . Likewise, because of the regular polygon's symmetry, a circle constructed to be inscribed in a regular polygon and touching the polygon will touch the regular polygon at the midpoint of the polygon side. As shown in the pictures, Figure 1 and Figure 2, lines from the regular polygon's vertices to the circle's center form n isosceles triangles of equal area.
The names of polygons vary based on the number of sides as follows:
- triangle - 3 sides
- square - 4 sides
- pentagon - 5 sides
- hexagon - 6 sides
- heptagon - 7 sides
- octagon - 8 sides
- nonagon - 9 sides
- decagon - 10 sides
- hendecagon - 11 sides
- dodecagon - 12 sides
Common Regular Polygon Functions
Polygon Area Calculators:
- Polygon Area from the Number of sides and Length of Sides
- Polygon Area from the Number of Sides and Outside Radius
- Area of a Polygon Segment (triangle) from the Number of Sides and Inscribed Radius
- Polygon Area from the Number of Sides and Inscribed Radius.
Polygon Side Calculators
- Length of a Polygon Side from the Number of Sides and Outer Radius
- Length of a Polygon Side from the Number of Sides and Inner Radius
- Length of a Polygon Side from the Number of Sides and Area in Poloygon
Polygon Perimeter Calculators
- Perimeter of a Polygon from Number of Sides and Length of Sides
- Perimeter of a Polygon from Number of Sides and Outer Radius
- Perimeter of a Polygon from Number of Sides and Inner Radius
- Polygon Perimeter from the Area and Number of Sides
Polygon Radius
3D Polygon Shapes
Other Polygon Calculators
- Interior Angle of a Regular Polygon based on the number of sides
- Area of Circle - Circle approximates a polygon as the number of sides approaches infinity.
- Area of Triangle - Three Sides
- Area of a Square - Four Sides
- Area of Pentagon - Five Sides
- Area of Hexagon - Six Sides
- Area of Heptagon - Seven Sides
- Area of Octagon - Eight Sides
- Area of Nonagon - Nine Sides
- Area of Decagon - Ten Sides
- Area of Hendecagon - Eleven Sides
- Area of Dodecagon - Twelve Sides