lever (beam length)

The Length of a Lever calculator (y = x • W/F ) 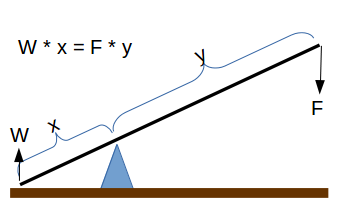computes the leverage length (y) on the downward force side of the fulcrum to lift an object by leverage.

INSTRUCTIONS:  Choose units and enter the following:

• (F)  Downward force (weight)
• (W) Weight of the object
• (x) Pivot length of the beam on the object's side of the fulcrum (see diagram)

Leverage Length (y): The calculator computes the length of the beam (y) in meters.  However this can be automatically converted to other length units via the pull-down menu.  The calculator also returns the pivot length (x) and the total length (x+y).

The Math/Science

A lever is a simple machine where the ratio of the product of the lengths and forces on opposite sides of a fulcrum are equal.

Mechanical Leverage Functions

• (y) Beam Length: computes the required length of a beam above the fulcrum for a lever to raise a weight (W) based on the downward weight applied (F) and the length below the fulcrum (x).
• (W) Lift Weight: computes the weight that can be lifted with a lever based on the length of the beam (y) above the fulcrum, the length (x) below the fulcrum and downward weight applied (F).
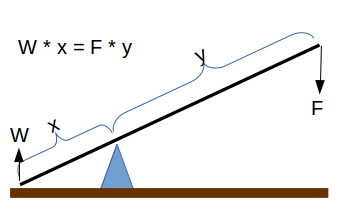
• (x) Fulcrum Position: computes the length from the object to the fulcrum needed in a lever to lift a weight (W) with a downward force (F) with a beam of length (L), where L = x + y (see below).
• (F) Downward Force or Weight: computes the mass needed to create the downward force (F) to raise the object with a lever.
• L = x+y : computes the sum of two lengths

If you set up a lever (beam and fulcrum), this formula will tell you the length needed to lift the mass.  Assume you put your full weight on the end of the beam, 200 lbs, and that you want to lift 1,400 lbs.  This formula will tell you that if there is 6" of the beam on the mass side of the fulcrum, you weight needs to be at the 3.5 foot (42 inches) mark on the other side to lift the object.

Simple Machine Calculators

• Lever Beam Length 
• Leverage Lift Weight 
• Fulcrum Position 
• Belt Length 
• Belt Speed
• RPMs to Linear Velocity
• RPMs from linear velocity and diameter 
• 2nd Pulley RPMs
• 2nd Pulley Diameter 
• RPM of 4th pulley on three shafts 
• 2nd Gear RPM 
• Sum of Two Lengths
• Second Gear Torque
• Leadscrew Torque (lift)