17.2 Simple harmonic motion by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
17.2 Simple harmonic motion
 Why are sine-wave vibrations so common?
Why are sine-wave vibrations so common?
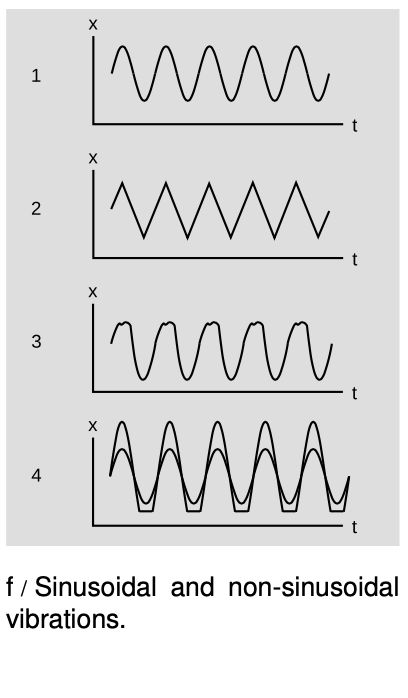
If we actually construct the mass-on-a-spring system discussed in the previous section and measure its motion accurately, we will find that its `x-t` graph is nearly a perfect sine-wave shape, as shown in figure f/1. (We call it a “sine wave” or “sinusoidal” even if it is a cosine, or a sine or cosine shifted by some arbitrary horizontal amount.) It may not be surprising that it is a wiggle of this general sort, but why is it a specific mathematically perfect shape? Why is it not a sawtooth shape like 2 or some other shape like 3? The mystery deepens as we find that a vast number of apparently unrelated vibrating systems show the same mathematical feature. A tuning fork, a sapling pulled to one side and released, a car bouncing on its shock absorbers, all these systems will exhibit sine-wave motion under one condition: the amplitude of the motion must be small.
It is not hard to see intuitively why extremes of amplitude would act differently. For example, a car that is bouncing lightly on its shock absorbers may behave smoothly, but if we try to double the amplitude of the vibrations the bottom of the car may begin hitting the ground, f/4. (Although we are assuming for simplicity in this chapter that energy is never dissipated, this is clearly not a very realistic assumption in this example. Each time the car hits the ground it will convert quite a bit of its potential and kinetic energy into heat and sound, so the vibrations would actually die out quite quickly, rather than repeating for many cycles as shown in the figure.)
The key to understanding how an object vibrates is to know how the force on the object depends on the object's position. If an object is vibrating to the right and left, then it must have a leftward force on it when it is on the right side, and a rightward force when it is on the left side. In one dimension, we can represent the direction of the force using a positive or negative sign, and since the force changes from positive to negative there must be a point in the middle where the force is zero. This is the equilibrium point, where the object would stay at rest if it was released at rest. For convenience of notation throughout this chapter, we will define the origin of our coordinate system so that `x` equals zero at equilibrium.
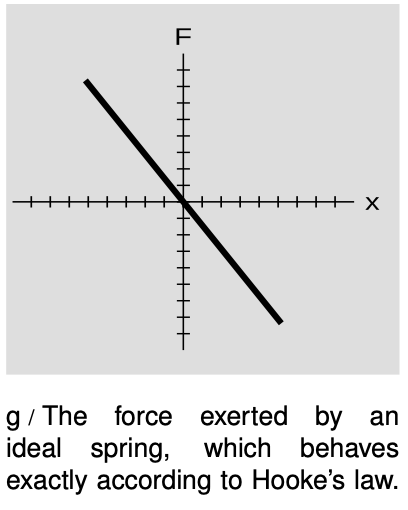 The simplest example is the mass on a spring, for which the force on the mass is given by Hooke's law,
The simplest example is the mass on a spring, for which the force on the mass is given by Hooke's law,
We can visualize the behavior of this force using a graph of `F` versus `x`, as shown in figure g. The graph is a line, and the spring constant, `k`, is equal to minus its slope. A stiffer spring has a larger value of `k` and a steeper slope. Hooke's law is only an approximation, but it works very well for most springs in real life, as long as the spring isn't compressed or stretched so much that it is permanently bent or damaged.
The following important theorem, whose proof is given in optional section 17.3, relates the motion graph to the force graph.
{Theorem: A linear force graph makes a sinusoidal motion graph.}
If the total force on a vibrating object depends only on the object's position, and is related to the objects displacement from equilibrium by an equation of the form `F_X=-kX`, then the object's motion displays a sinusoidal graph with period `T=2pisqrt(m/k)`
 Even if you do not read the proof, it is not too hard to understand why the equation for the period makes sense. A greater mass causes a greater period, since the force will not be able to whip a massive object back and forth very rapidly. A larger value of `k` causes a shorter period, because a stronger force can whip the object back and forth more rapidly.
Even if you do not read the proof, it is not too hard to understand why the equation for the period makes sense. A greater mass causes a greater period, since the force will not be able to whip a massive object back and forth very rapidly. A larger value of `k` causes a shorter period, because a stronger force can whip the object back and forth more rapidly.
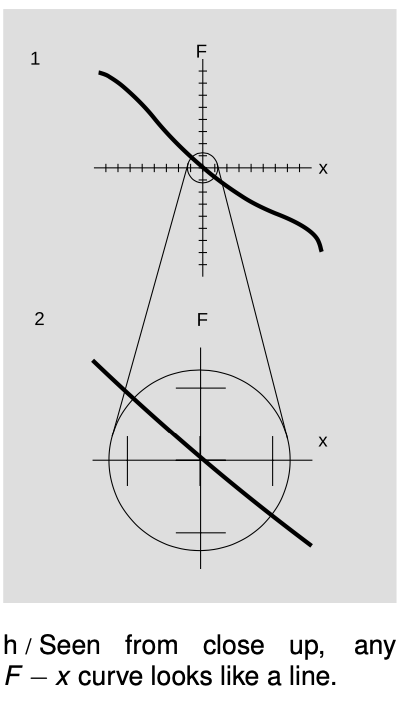
This may seem like only an obscure theorem about the mass-on-a-spring system, but figure h shows it to be far more general than that. Figure h/1 depicts a force curve that is not a straight line. A system with this `F`-`x` curve would have large-amplitude vibrations that were complex and not sinusoidal. But the same system would exhibit sinusoidal small-amplitude vibrations. This is because any curve looks linear from very close up. If we magnify the `F`-`x` graph as shown in figure h/2, it becomes very difficult to tell that the graph is not a straight line. If the vibrations were confined to the region shown in h/2, they would be very nearly sinusoidal. This is the reason why sinusoidal vibrations are a universal feature of all vibrating systems, if we restrict ourselves to small amplitudes. The theorem is therefore of great general significance. It applies throughout the universe, to objects ranging from vibrating stars to vibrating nuclei. A sinusoidal vibration is known as simple harmonic motion.
Period is approximately independent of amplitude, if the amplitude is small.
Until now we have not even mentioned the most counterintuitive aspect of the equation `T=2pisqrt(m/k)`: it does not depend on amplitude at all. Intuitively, most people would expect the mass-on-a-spring system to take longer to complete a cycle if the amplitude was larger. (We are comparing amplitudes that are different from each other, but both small enough that the theorem applies.) In fact the larger-amplitude vibrations take the same amount of time as the small-amplitude ones. This is because at large amplitudes, the force is greater, and therefore accelerates the object to higher speeds.
Legend has it that this fact was first noticed by Galileo during what was apparently a less than enthralling church service. A gust of wind would now and then start one of the chandeliers in the cathedral swaying back and forth, and he noticed that regardless of the amplitude of the vibrations, the period of oscillation seemed to be the same. Up until that time, he had been carrying out his physics experiments with such crude time-measuring techniques as feeling his own pulse or singing a tune to keep a musical beat. But after going home and testing a pendulum, he convinced himself that he had found a superior method of measuring time. Even without a fancy system of pulleys to keep the pendulum's vibrations from dying down, he could get very accurate time measurements, because the gradual decrease in amplitude due to friction would have no effect on the pendulum's period. (Galileo never produced a modern-style pendulum clock with pulleys, a minute hand, and a second hand, but within a generation the device had taken on the form that persisted for hundreds of years after.)
Example 4: The pendulum
`=>` Compare the periods of pendula having bobs with different masses.
`=>` From the equation `T=2pisqrt(m/k)`, we might expect that a larger mass would lead to a longer period. However, increasing the mass also increases the forces that act on the pendulum: gravity and the tension in the string. This increases `k` as well as `m`, so the period of a pendulum is independent of `m`.
Discussion Questions
A Suppose that a pendulum has a rigid arm mounted on a bearing, rather than a string tied at its top with a knot. The bob can then oscillate with center-to-side amplitudes greater than `90°`. For the maximum amplitude of `180°`, what can you say about the period?
B In the language of calculus, Newton's second law for a simple harmonic oscillator can be written in the form `d^2``x`/`dt^2`=-(...) `x`, where "..." refers to a constant, and the minus sign says that if we pull the object away from equilibrium, a restoring force tries to bring it back to equilibrium, which is the opposite direction. This is why we get motion that looks like a sine or cosine function: these are functions that, when differentiated twice, give back the original function but with an opposite sign. Now consider the example described in discussion question A, where a pendulum is upright or nearly upright. How does the analysis play out differently?
17.2 Simple harmonic motion by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.