The Hooke's Law Calculator computes the force to compress or extend a spring (Fx) to compress or extend a spring based on the spring constant (k) for the spring and a specified length (x).
INSTRUCTIONS:: Choose units and enter the following:
- (x) Distance of compression or extension
- (k) Spring constant
Force to Compress a Spring (Fx): The calculator computes the required force (Fx) in Newtons. However, this can be automatically converted to other force units via the pull-down menu.
The Math
Hooke's Law relates the restoring force, F, needed to extend or compress a spring to the length, X. The force can be applied to either extension or compression of the spring. The extension/compression is proportional to the force required and the constant, k, is characteristic of the spring's stiffness.
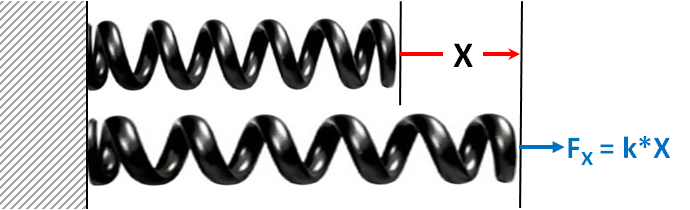A compressed Spring
Force in this equation is directly proportional to elongation -- IFF the elongation is not too great. In other words if you stretch the spring with too much force, you can cause permanent deformation of the spring and the spring constant is altered.
Remember those Slinkys from when you were a kid that were damaged when they were stretched too far?
To stretch the spring we must do work and thus we get the associated equation W = ½• k•X².
Spring Equation Calculators
- Period of an Oscillating Spring: This computes the period of oscillation of a spring based on the spring constant and mass.
- Mass of a Spring: This computes the mass based on the spring constant and the period of oscillation.
- Angular Frequency of a Spring: This computes the angular frequency based on the spring constant and the mass.
- Spring Constant: This computes a spring's constant based on the mass and period of oscillation.
- Work done on a Spring: This computes the work based on the spring constant and the two positions of a spring.
- Hooke's Law: This computes the force to change the length of a spring based on the spring constant and length of displacement.
- Force to Fully Compress a Spring: This computes the force required to fully compress a spring based on the spring's physical attributes including the Young's Modulus, wire diameter, length of spring, number of windings, Poisson ratio, and outer diameter of the spring.
EXTERNAL LINKS
Khan Academy's Intro to springs and Hooke's Law