`A = y/sin(kx+omegat+phi)`

Enter a value for all fields

The Amplitude of a wave equation computes the amplitude of a wave using the wave number(k), displacement of the wave(x), the angular frequency(`omega`), the time passed(t), and the phase angle(`phi`).

INSTRUCTIONS: Choose units and enter the following:

• (y) Wave Displacement
• (x) Wave Distance
• (k) Wave Number (in rad/m)
• (w) Angular Frequency
• (t) Time
• (p) Phase Constant

Amplitude(A): The calculator returns amplitude(A) in meters. However, this can be automatically converted to other amplitude units via the pull-down menu.

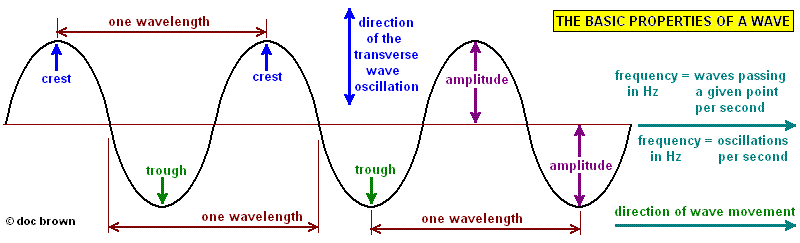The Math / Science

This equation comes from the basic wave equation:

`y(x,t) = Asin(kx+wt+phi)`

where,

• y(x,t) are the parameters of the wave
• A is the amplitude
• k is the wave number
• x is the wave distance
• w is the angular frequency
• t is the time passed
• `phi` is the phase angle.

Some simple Algebra allows us to gain the equation that you see at the top of the page:

`A = y/sin(kx+wt+phi)`

Notes: 

 Please enter the wave number in the units of radians-per-meter as it won't compute properly in different units.

References:

Light and Matter Chapter 17: Vibrations