The Trace of a 3X3 Matrix calculator computes the trace (Tr) of a 3x3 matrix (A). 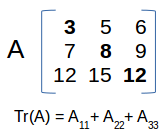
INSTRUCTIONS: Enter the following
- (A) The 3x3 matrix.
TRACE: The calculator computes the trace of the 3x3 matrix.
Matrix Calculators
- Determinant of 3-by-3 Matrix
- Characteristic Polynomial of a 3x3 matrix
- Inverse of a 3x3 Matrix
- Transpose of a 3x3 Matrix
- Trace of a 3x3 Matrix
- Mirror of a 3x3 Matrix
- 3x3 Matrix Characteristics (Trace, Determinant, Inverse, Characteristic Polynomial)
- Product of a 3x3 matrix and a Scalar
- Product of a 3x3 matrix and a 3x1 matrix
- Product of two 3x3 matrices
- Solving 3 Equations with 3 Unknowns
- Cramer's Rule (three equations, solved for x, y and z)
- Cramer's Rule Calculator
Trace of 3X3 Matrix
[Math | Numerical Analysis | Matrices] This equation computes the trace of a three-by-three matrix.
Given a square matrix where:
A = `[[A_11,A_12,A_13],[A_21,A_22,A_23],[A_31,A_32,A_33]]` ,
the Trace of this matrix is defined as:
tr (A) = `A_11` + `A_22`+ `A_33`
The trace can be used in a number of numerical analyses computing things like the eigenvalues of a matrix.
Notes
The trace of a square matrix (the matrix must be a square matrix) is simply the sum of the diagonals: `A_11 + A_22 +` ... `A_nn`.
Note that the trace of a matrix is equal to that of its transpose, i.e., tr(A) = tr(AT)
