5.7 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
repulsive — describes a force that tends to push the two participating objects apart
attractive — describes a force that tends to pull the two participating objects together
oblique — describes a force that acts at some other angle, one that is not a direct repulsion or attraction
normal force — the force that keeps two objects from occupying the same space
static friction — a friction force between surfaces that are not slipping past each other
kinetic friction — a friction force between surfaces that are slipping past each other
fluid — a gas or a liquid
fluid friction — a friction force in which at least one of the object is a fluid
spring constant — the constant of proportionality between force and elongation of a spring or other object under strain
Notation
`F_N` — a normal force
`F_s` — a static frictional force
`F_k` — a kinetic frictional force
`mu_s` — the coefficient of static friction; the constant of proportionality between the maximum static frictional force and the normal force; depends on what types of surfaces are involved
`mu_k` — the coefficient of kinetic friction; the constant of proportionality between the kinetic frictional force and the normal force; depends on what types of surfaces are involved
`k` — the spring constant; the constant of proportionality between the force exerted on an object and the amount by which the object is lengthened or compressed
Summary
Newton's third law states that forces occur in equal and opposite pairs. If object A exerts a force on object B, then object B must simultaneously be exerting an equal and opposite force on object A. Each instance of Newton's third law involves exactly two objects, and exactly two forces, which are of the same type.
There are two systems for classifying forces. We are presently using the more practical but less fundamental one. In this system, forces are classified by whether they are repulsive, attractive, or oblique; whether they are contact or noncontact forces; and whether the two objects involved are solids or fluids.
Static friction adjusts itself to match the force that is trying to make the surfaces slide past each other, until the maximum value is reached,
Once this force is exceeded, the surfaces slip past one another, and kinetic friction applies,
Both types of frictional force are nearly independent of surface area, and kinetic friction is usually approximately independent of the speed at which the surfaces are slipping. The direction of the force is in the direction that would tend to stop or prevent slipping.
A good first step in applying Newton's laws of motion to any physical situation is to pick an object of interest, and then to list all the forces acting on that object. We classify each force by its type, and find its Newton's-third-law partner, which is exerted by the object on some other object.
When two objects are connected by a third low-mass object, their forces are transmitted to each other nearly unchanged.
Objects under strain always obey Hooke's law to a good approximation, as long as the force is small. Hooke's law states that the stretching or compression of the object is proportional to the force exerted on it,
`F~~k(x-xo)`.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
 1. A little old lady and a pro football player collide head-on. Compare their forces on each other, and compare their accelerations. Explain.
1. A little old lady and a pro football player collide head-on. Compare their forces on each other, and compare their accelerations. Explain.
2. The earth is attracted to an object with a force equal and opposite to the force of the earth on the object. If this is true, why is it that when you drop an object, the earth does not have an acceleration equal and opposite to that of the object?
3. When you stand still, there are two forces acting on you, the force of gravity (your weight) and the normal force of the floor pushing up on your feet. Are these forces equal and opposite? Does Newton's third law relate them to each other? Explain.
 In problems 4-8, analyze the forces using a table in the format shown in section 5.3. Analyze the forces in which the italicized object participates.
In problems 4-8, analyze the forces using a table in the format shown in section 5.3. Analyze the forces in which the italicized object participates.
4. Some people put a spare car key in a little magnetic box that they stick under the chassis of their car. Let's say that the box is stuck directly underneath a horizontal surface, and the car is parked. (See instructions above.)
5. Analyze two examples of objects at rest relative to the earth that are being kept from falling by forces other than the normal force. Do not use objects in outer space, and do not duplicate problem 4 or 8. (See instructions above.)
 6. A person is rowing a boat, with her feet braced. She is doing the part of the stroke that propels the boat, with the ends of the oars in the water (not the part where the oars are out of the water). (See instructions above.)
6. A person is rowing a boat, with her feet braced. She is doing the part of the stroke that propels the boat, with the ends of the oars in the water (not the part where the oars are out of the water). (See instructions above.)
7. A farmer is in a stall with a cow when the cow decides to press him against the wall, pinning him with his feet off the ground. Analyze the forces in which the farmer participates. (See instructions above.)
8. A propeller plane is cruising east at constant speed and altitude. (See instructions above.)
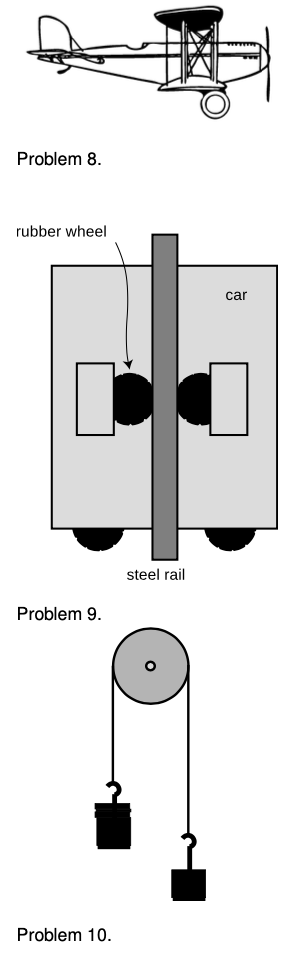
9. Today's tallest buildings are really not that much taller than the tallest buildings of the 1940's. One big problem with making an even taller skyscraper is that every elevator needs its own shaft running the whole height of the building. So many elevators are needed to serve the building's thousands of occupants that the elevator shafts start taking up too much of the space within the building. An alternative is to have elevators that can move both horizontally and vertically: with such a design, many elevator cars can share a few shafts, and they don't get in each other's way too much because they can detour around each other. In this design, it becomes impossible to hang the cars from cables, so they would instead have to ride on rails which they grab onto with wheels. Friction would keep them from slipping. The figure shows such a frictional elevator in its vertical travel mode. (The wheels on the bottom are for when it needs to switch to horizontal motion.)
(a) If the coefficient of static friction between rubber and steel is `mu_s`, and the maximum mass of the car plus its passengers is `M`, how much force must there be pressing each wheel against the rail in order to keep the car from slipping? (Assume the car is not accelerating.)(answer check available at lightandmatter.com)
(b) Show that your result has physically reasonable behavior with respect to `mu_s`. In other words, if there was less friction, would the wheels need to be pressed more firmly or less firmly? Does your equation behave that way?
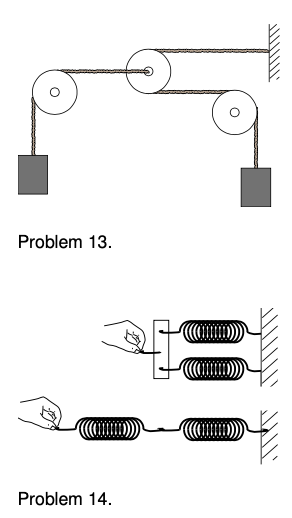
10. Unequal masses `M` and `m` are suspended from a pulley as shown in the figure.
(a) Analyze the forces in which mass `m` participates, using a table in the format shown in section 5.3. [The forces in which the other mass participates will of course be similar, but not numerically the same.]
(b) Find the magnitude of the accelerations of the two masses. [Hints: (1) Pick a coordinate system, and use positive and negative signs consistently to indicate the directions of the forces and accelerations. (2) The two accelerations of the two masses have to be equal in magnitude but of opposite signs, since one side eats up rope at the same rate at which the other side pays it out. (3) You need to apply Newton's second law twice, once to each mass, and then solve the two equations for the unknowns: the acceleration, `a`, and the tension in the rope, `T` (answer check available at lightandmatter.com)
(c) Many people expect that in the special case of `M=m`, the two masses will naturally settle down to an equilibrium position side by side. Based on your answer from part b, is this correct?
(d) Find the tension in the rope, `T`.(answer check available at lightandmatter.com)
(e) Interpret your equation from part d in the special case where one of the masses is zero. Here “interpret” means to figure out what happens mathematically, figure out what should happen physically, and connect the two.
11. A tugboat of mass `m` pulls a ship of mass `M`, accelerating it. The speeds are low enough that you can ignore fluid friction acting on their hulls, although there will of course need to be fluid friction acting on the tug's propellers.
(a) Analyze the forces in which the tugboat participates, using a table in the format shown in section 5.3. Don't worry about vertical forces.
(b) Do the same for the ship.
(c) If the force acting on the tug's propeller is `F`, what is the tension, `T`, in the cable connecting the two ships? [Hint: Write down two equations, one for Newton's second law applied to each object. Solve these for the two unknowns `T` and `a`](answer check available at lightandmatter.com)
(d) Interpret your answer in the special cases of `M=0` and `M=infty`.
12. Someone tells you she knows of a certain type of Central American earthworm whose skin, when rubbed on polished diamond, has `mu_k`>`mu_s`. Why is this not just empirically unlikely but logically suspect?
 13. In the system shown in the figure, the pulleys on the left and right are fixed, but the pulley in the center can move to the left or right. The two masses are identical. Show that the mass on the left will have an upward acceleration equal to `g"/"5`. Assume all the ropes and pulleys are massless and frictionless.
13. In the system shown in the figure, the pulleys on the left and right are fixed, but the pulley in the center can move to the left or right. The two masses are identical. Show that the mass on the left will have an upward acceleration equal to `g"/"5`. Assume all the ropes and pulleys are massless and frictionless.
14. The figure shows two different ways of combining a pair of identical springs, each with spring constant `k`. We refer to the top setup as parallel, and the bottom one as a series arrangement.
(a) For the parallel arrangement, analyze the forces acting on the connector piece on the left, and then use this analysis to determine the equivalent spring constant of the whole setup. Explain whether the combined spring constant should be interpreted as being stiffer or less stiff.
(b) For the series arrangement, analyze the forces acting on each spring and figure out the same things.(solution in the pdf version of the book)
15. Generalize the results of problem 14 to the case where the two spring constants are unequal.
16. (a) Using the solution of problem 14, which is given in the back of the book, predict how the spring constant of a fiber will depend on its length and cross-sectional area.
(b) The constant of proportionality is called the Young's modulus, `E`, and typical values of the Young's modulus are about `10^10` to `10^11`. What units would the Young's modulus have in the SI (meter-kilogram-second) system? (solution in the pdf version of the book)
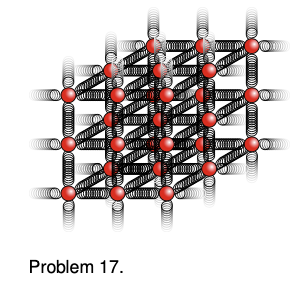 17. This problem depends on the results of problems 14 and 16, whose solutions are in the back of the book. When atoms form chemical bonds, it makes sense to talk about the spring constant of the bond as a measure of how “stiff” it is. Of course, there aren't really little springs --- this is just a mechanical model. The purpose of this problem is to estimate the spring constant, `k`, for a single bond in a typical piece of solid matter. Suppose we have a fiber, like a hair or a piece of fishing line, and imagine for simplicity that it is made of atoms of a single element stacked in a cubical manner, as shown in the figure, with a center-to-center spacing `b`. A typical value for `b` would be about `10^(?10) m`.
17. This problem depends on the results of problems 14 and 16, whose solutions are in the back of the book. When atoms form chemical bonds, it makes sense to talk about the spring constant of the bond as a measure of how “stiff” it is. Of course, there aren't really little springs --- this is just a mechanical model. The purpose of this problem is to estimate the spring constant, `k`, for a single bond in a typical piece of solid matter. Suppose we have a fiber, like a hair or a piece of fishing line, and imagine for simplicity that it is made of atoms of a single element stacked in a cubical manner, as shown in the figure, with a center-to-center spacing `b`. A typical value for `b` would be about `10^(?10) m`.
(a) Find an equation for `k` in terms of `b`, and in terms of the Young's modulus,`E`, defined in problem 16 and its solution.
(b) Estimate `k` using the numerical data given in problem 16.
(c) Suppose you could grab one of the atoms in a diatomic molecule like `H_2` or `O_2`, and let the other atom hang vertically below it. Does the bond stretch by any appreciable fraction due to gravity?
18. (solution in the pdf version of the book) In each case, identify the force that causes the acceleration, and give its Newton's-third-law partner. Describe the effect of the partner force. (a) A swimmer speeds up. (b) A golfer hits the ball off of the tee. (c) An archer fires an arrow. (d) A locomotive slows down. `=>` Solution, p. 539
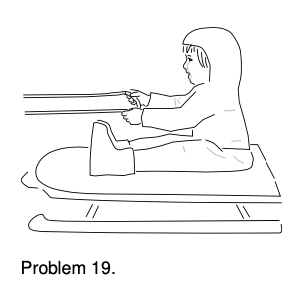 19. Ginny has a plan. She is going to ride her sled while her dog Foo pulls her, and she holds on to his leash. However, Ginny hasn't taken physics, so there may be a problem: she may slide right off the sled when Foo starts pulling.
19. Ginny has a plan. She is going to ride her sled while her dog Foo pulls her, and she holds on to his leash. However, Ginny hasn't taken physics, so there may be a problem: she may slide right off the sled when Foo starts pulling.
(a) Analyze all the forces in which Ginny participates, making a table as in section 5.3.
(b) Analyze all the forces in which the sled participates.
(c) The sled has mass `m`, and Ginny has mass `M`. The coefficient of static friction between the sled and the snow is `mu_1`, and `mu_2` is the corresponding quantity for static friction between the sled and her snow pants. Ginny must have a certain minimum mass so that she will not slip off the sled. Find this in terms of the other three variables.(answer check available at lightandmatter.com)
(d) Interpreting your equation from part c, under what conditions will there be no physically realistic solution for `M`? Discuss what this means physically.
20. (solution in the pdf version of the book) Example 2 on page 157 involves a person pushing a box up a hill. The incorrect answer describes three forces. For each of these three forces, give the force that it is related to by Newton's third law, and state the type of force.
21. Example 10 on page 176 describes a force-doubling setup involving a pulley. Make up a more complicated arrangement, using two pulleys, that would multiply the force by four. The basic idea is to take the output of one force doubler and feed it into the input of a second one.
22. Pick up a heavy object such as a backpack or a chair, and stand on a bathroom scale. Shake the object up and down. What do you observe? Interpret your observations in terms of Newton's third law.
23. A cop investigating the scene of an accident measures the length `L` of a car's skid marks in order to find out its speed `v` at the beginning of the skid. Express `v` in terms of `L` and any other relevant variables.(answer check available at lightandmatter.com)
24. The following reasoning leads to an apparent paradox; explain what's wrong with the logic. A baseball player hits a ball. The ball and the bat spend a fraction of a second in contact. During that time they're moving together, so their accelerations must be equal. Newton's third law says that their forces on each other are also equal. But `a=F"/"m`, so how can this be, since their masses are unequal? (Note that the paradox isn't resolved by considering the force of the batter's hands on the bat. Not only is this force very small compared to the ball-bat force, but the batter could have just thrown the bat at the ball.)
25. This problem has been deleted.
26. (solution in the pdf version of the book) (a) Compare the mass of a one-liter water bottle on earth, on the moon, and in interstellar space.
(b) Do the same for its weight.
27. An ice skater builds up some speed, and then coasts across the ice passively in a straight line. (a) Analyze the forces, using a table in the format shown in section 5.3.
(b) If his initial speed is `v`, and the coefficient of kinetic friction is `mu_k`, find the maximum theoretical distance he can glide before coming to a stop. Ignore air resistance.(answer check available at lightandmatter.com)
(c) Show that your answer to part b has the right units.
(d) Show that your answer to part b depends on the variables in a way that makes sense physically.
(e) Evaluate your answer numerically for `mu_k=0.0046`, and a world-record speed of `14.58 m"/"s`. (The coefficient of friction was measured by De Koning et al., using special skates worn by real speed skaters.)(answer check available at lightandmatter.com)
(f) Comment on whether your answer in part e seems realistic. If it doesn't, suggest possible reasons why.
 28. Mountain climbers with masses `m` and `M` are roped together while crossing a horizontal glacier when a vertical crevasse opens up under the climber with mass `M`. The climber with mass `m` drops down on the snow and tries to stop by digging into the snow with the pick of an ice ax. Alas, this story does not have a happy ending, because this doesn't provide enough friction to stop. Both `m` and `M` continue accelerating, with `M` dropping down into the crevasse and `m` being dragged across the snow, slowed only by the kinetic friction with coefficient `mu_k` acting between the ax and the snow. There is no significant friction between the rope and the lip of the crevasse.
28. Mountain climbers with masses `m` and `M` are roped together while crossing a horizontal glacier when a vertical crevasse opens up under the climber with mass `M`. The climber with mass `m` drops down on the snow and tries to stop by digging into the snow with the pick of an ice ax. Alas, this story does not have a happy ending, because this doesn't provide enough friction to stop. Both `m` and `M` continue accelerating, with `M` dropping down into the crevasse and `m` being dragged across the snow, slowed only by the kinetic friction with coefficient `mu_k` acting between the ax and the snow. There is no significant friction between the rope and the lip of the crevasse.
(a) Find the acceleration `a`.(answer check available at lightandmatter.com)
(b) Check the units of your result.
(c) Check the dependence of your equation on the variables. That means that for each variable, you should determine what its effect on `a` should be physically, and then what your answer from part a says its effect would be mathematically.
29. The figure shows a column in the shape of a woman, holding up the roof of part of the Parthenon. Analyze the forces in which she participates, using a table in the format shown in section 5.3.(solution in the pdf version of the book)
30. Problem 15, p. 150, which has a solution in the back of the book, was an analysis of the forces acting on a rock climber being lowered back down on the rope. Expand that analysis into a table in the format shown in section 5.3, which includes the types of the forces and their Newton's-third-law partners.
31. The figure shows a man trying to push his car out of the mud. (a) Suppose that he isn't able to move the car. Analyze the forces in which the car participates, using a table in the format shown in section 5.3. (b) Suppose instead that the man is able to move the car, and the car is currently moving at constant speed. Discuss the strengths of the forces in relation to one another, and compare with what happened in part a. (c) The man gets tired. He is still pushing, but the car, although still moving, begins to decelerate. Discuss this as in part b.
5.7 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.