3.3 Positive and Negative Acceleration by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
3.3 Positive and negative acceleration
Gravity always pulls down, but that does not mean it always speeds things up. If you throw a ball straight up, gravity will first slow it down to `v=0` and then begin increasing its speed. When I took physics in high school, I got the impression that positive signs of acceleration indicated speeding up, while negative accelerations represented slowing down, i.e., deceleration. Such a definition would be inconvenient, however, because we would then have to say that the same downward tug of gravity could produce either a positive or a negative acceleration. As we will see in the following example, such a definition also would not be the same as the slope of the `v-t` graph.
Let's study the example of the rising and falling ball. In the example of the person falling from a bridge, I assumed positive velocity values without calling attention to it, which meant I was assuming a coordinate system whose `x` axis pointed down. In this example, where the ball is reversing direction, it is not possible to avoid negative velocities by a tricky choice of axis, so let's make the more natural choice of an axis pointing up. The ball's velocity will initially be a positive number, because it is heading up, in the same direction as the x axis, but on the way back down, it will be a negative number. As shown in the figure, the `v-t` graph does not do anything special at the top of the ball's flight, where `v` equals 0. Its slope is always negative. In the left half of the graph, there is a negative slope because the positive velocity is getting closer to zero. On the right side, the negative slope is due to a negative velocity that is getting farther from zero, so we say that the ball is speeding up, but its velocity is decreasing!
To summarize, what makes the most sense is to stick with the original definition of acceleration as the slope of the `v-t` graph, Δv/Δt. By this definition, it just isn't necessarily true that things speeding up have positive acceleration while things slowing down have negative acceleration. The word “deceleration” is not used much by physicists, and the word “acceleration” is used unblushingly to refer to slowing down as well as speeding up: “There was a red light, and we accelerated to a stop.”
Example 4: Numerical calculation of a negative acceleration
⇒ In figure i, what happens if you calculate the acceleration between `t=1.0` and `1.5 "s"`?
⇒ Reading from the graph, it looks like the velocity is about `-1 "m/s"` at `t=1.0 "s"`, and around `-6 "m/s"` at `t=1.5 "s"`. The acceleration, figured between these two points, is
`a=(Deltav)/(Deltat)`=`"(-6 m/s)-(-1 m/s)"/ "(1.5 s)-(1.0 s)"=-10 "m/s"^2`.
Even though the ball is speeding up, it has a negative acceleration.
Another way of convincing you that this way of handling the plus and minus signs makes sense is to think of a device that measures acceleration. After all, physics is supposed to use operational definitions, ones that relate to the results you get with actual measuring devices. Consider an air freshener hanging from the rear-view mirror of your car. When you speed up, the air freshener swings backward. Suppose we define this as a positive reading. When you slow down, the air freshener swings forward, so we'll call this a negative reading on our accelerometer. But what if you put the car in reverse and start speeding up backwards? Even though you're speeding up, the accelerometer responds in the same way as it did when you were going forward and slowing down. There are four possible cases:
| motion of car | accelerometer swings | slope of v-t graph | direction of force acting on car |
| forward, speeding up | backward | + | forward |
| forward, slowing down | forward | - | backward |
| backward, speeding up | forward | - | backward |
| backward, slowing down | backward | + | forward |
Note the consistency of the three right-hand columns --- nature is trying to tell us that this is the right system of classification, not the left-hand column.
Because the positive and negative signs of acceleration depend on the choice of a coordinate system, the acceleration of an object under the influence of gravity can be either positive or negative. Rather than having to write things like g =9.8m/s2 or -9.8 m/s2 every time we want to discuss g's numerical value, we simply define g as the absolute value of the acceleration of objects moving under the influence of gravity. We consistently let g=9.8 m/s2, but we may have either a = g or a =-g, depending on our choice of a coordinate system.
Example 5: Acceleration with a change in direction of motion
⇒ A person kicks a ball, which rolls up a sloping street, comes to a halt, and rolls back down again. The ball has constant acceleration. The ball is initially moving at a velocity of 4.0 m/s, and after 10.0 s it has returned to where it started. At the end, it has sped back up to the same speed it had initially, but in the opposite direction. What was its acceleration?
⇒ By giving a positive number for the initial velocity, the statement of the question implies a coordinate axis that points up the slope of the hill. The “same” speed in the opposite direction should therefore be represented by a negative number, -4.0 m/s. The acceleration is
a=`Deltav`/`Deltat`
=(`v_f`-`v_o`)/10.0 s
=[(-4.0 m/s)-(4.0 m/s)]/10.0s
=-0.80 m/`s^2`.
The acceleration was no different during the upward part of the roll than on the downward part of the roll.
Incorrect solution: Acceleration is Δv/Δt, and at the end it's not moving any faster or slower than when it started, so Δy=0 and a=0.
The velocity does change, from a positive number to a negative number.
Discussion Questions
A A child repeatedly jumps up and down on a trampoline. Discuss the sign and magnitude of his acceleration, including both the time when he is in the air and the time when his feet are in contact with the trampoline.
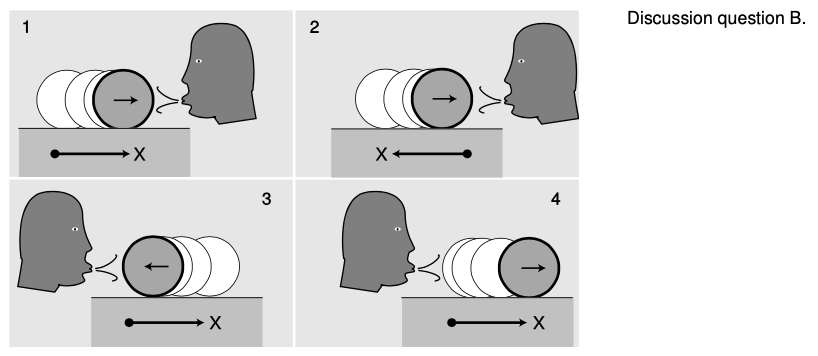
B The figure shows a refugee from a Picasso painting blowing on a rolling water bottle. In some cases the person's blowing is speeding the bottle up, but in others it is slowing it down. The arrow inside the bottle shows which direction it is going, and a coordinate system is shown at the bottom of each figure. In each case, figure out the plus or minus signs of the velocity and acceleration. It may be helpful to draw a `v-t` graph in each case.
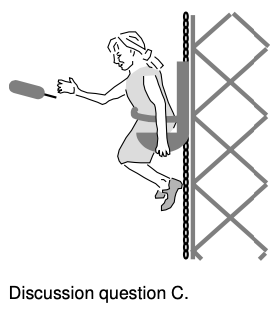 C Sally is on an amusement park ride which begins with her chair being hoisted straight up a tower at a constant speed of 60 miles/hour. Despite stern warnings from her father that he'll take her home the next time she misbehaves, she decides that as a scientific experiment she really needs to release her corndog over the side as she's on the way up. She does not throw it. She simply sticks it out of the car, lets it go, and watches it against the background of the sky, with no trees or buildings as reference points. What does the corndog's motion look like as observed by Sally? Does its speed ever appear to her to be zero? What acceleration does she observe it to have: is it ever positive? negative? zero? What would her enraged father answer if asked for a similar description of its motion as it appears to him, standing on the ground?
C Sally is on an amusement park ride which begins with her chair being hoisted straight up a tower at a constant speed of 60 miles/hour. Despite stern warnings from her father that he'll take her home the next time she misbehaves, she decides that as a scientific experiment she really needs to release her corndog over the side as she's on the way up. She does not throw it. She simply sticks it out of the car, lets it go, and watches it against the background of the sky, with no trees or buildings as reference points. What does the corndog's motion look like as observed by Sally? Does its speed ever appear to her to be zero? What acceleration does she observe it to have: is it ever positive? negative? zero? What would her enraged father answer if asked for a similar description of its motion as it appears to him, standing on the ground?
D Can an object maintain a constant acceleration, but meanwhile reverse the direction of its velocity?
E Can an object have a velocity that is positive and increasing at the same time that its acceleration is decreasing?
3.3 Positive and Negative Acceleration by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.