The Linear Eccentricity of an Ellipse calculator computes the linear eccentricity (f) of an ellipse which is the distance between the center point of the ellipse and either foci (F1 and F2). For the Eccentricity of an Ellipse, CLICK HERE.
INSTRUCTIONS: Choose units and enter the following;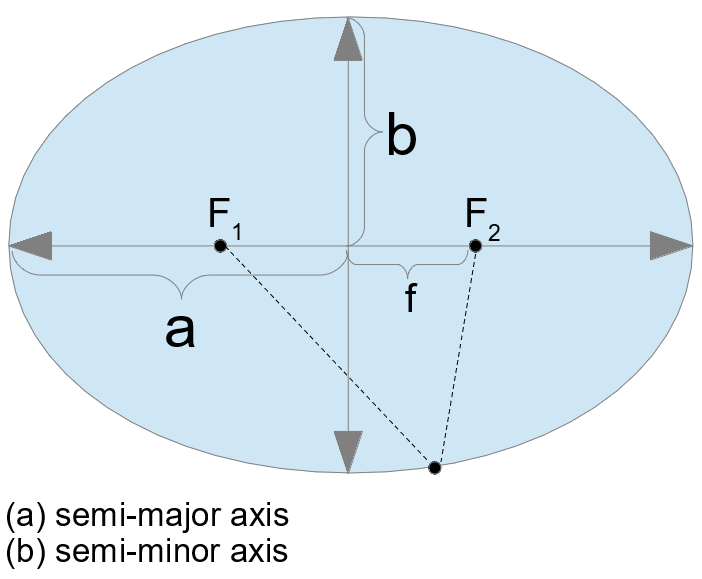
- (a) Semi-major axis length
- (b) Semi-minor axis length
Linear eccentricity of the ellipse (f): The calculator returns the value in meters. However, this can be automatically converted into numerous other length units (e.g. feet or inches) via the pull-down menu.
Notes on an Ellipse
Here's a visual representation of the creation of an ellipse:
As the representation shows you need something like a string that is attached to two fixed points. The moving black point can be your pen stretching the sting as it moves around the ellipse. The two fixed green points are actually the foci of the ellipse and so the line drawn through the two fixed points and which intersects the ellipse at both extremes is the major axis of the ellipse.
References
- Animation of the elipse is from: https://lh6.googleusercontent.com/-Gf58RKtiaoI/U4cZL6DxLzI/AAAAAAAAAE4/ymfjN-8bPOA/w506-h285/ellipse.gif
Related Ellipse calculators
- Area of an Ellipse: This computes the area of an ellipse based on the length of the axes.
- Rumanujan's Circumference of an Ellipse 1: This is the first of two of Rumanujan's approximations of the circumference (perimeter) of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
- Rumanujan's Circumference of an Ellipse 2: This is the second of Rumanujan approximations of the circumference (perimeter) of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
- Circumference of an Ellipse (other) This is another common estimation of the circumference (perimeter) of an ellipse based on the semi-major axis (a) and the semi-minor axis (b).
Conic Sections - Eccentricity of an Ellipse: This computes the eccentricity of an ellipse which is based on the ratios of the semi-major axis (a) and the semi-minor axis (b).
- Mean Radius of an Ellipse: This compute the mean radius of an ellipse. This would define a circle with the same approximate area, based on the ellipse's semi-major axis (a) and the semi-minor axis (b).
- Linear Eccentricity of an Ellipse: This computes the linear eccentricity of an ellipse.