The Acceleration Due to Gravity at a Latitude calculator estimates the acceleration due to gravity on Earth at a specific latitude above or below the equator.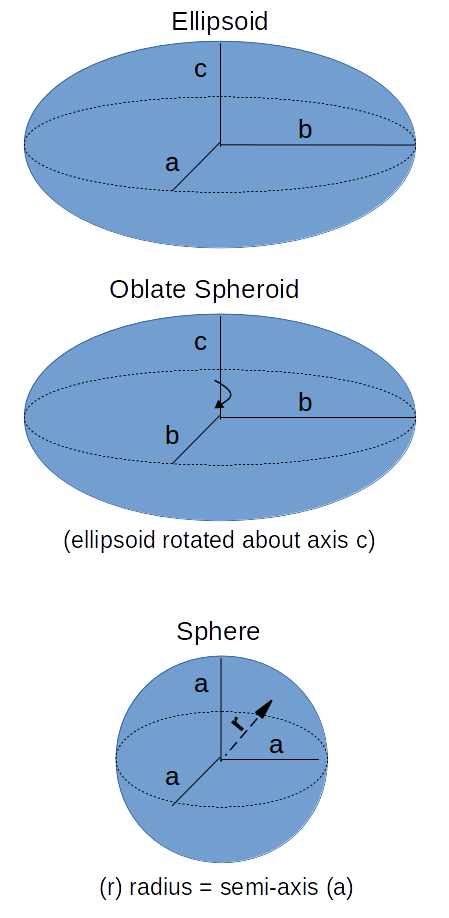
INSTRUCTIONS: Choose units and enter the following:
- (Φ) Latitude (angle from the equator)
Acceleration Due to Gravity (gLat): The calculator returns the acceleration in meters per second squared. However, this can be automatically converted to compatible units via the pull-down menu.
The Math / Science
The International Gravity formula computes the approximate acceleration due to gravity on the surface of the Earth at Sea Level based on the latitude. The results are returned in meters per second squared, but can be converted to numerous units via the pull-down menu.
The formula for the Acceleration Due to Gravity at a Latitude is:
`g_(Lat) = 9.7803267714*( (1+ 0.00193185138639*sin^2(phi))/sqrt(1- 0.00669437999013* sin^2(phi)))`
where:
- gLat = Acceleration Due to Gravity at the latitude
- Φ - Latitude
The earth is not a perfect sphere, because of the effect of the Earth's rotation and the resulting centrifugal force has caused the Earth to have a bulge around the equator, the Earth is more approximately an oblate spheroid. The Earth's rotation and the resultant centrifugal force (heading outward) counteracts the effect of gravity (downward). This has a measurable in the apparent acceleration due to gravity. A good approximation of the total effect is modeled in the International Gravity Formula above. To indicate the ascension or decline from the equator, latitude (φ) can be used.
