The AREA and PERIMETER (circumference) calculator provides equations for the area and perimeters of circles 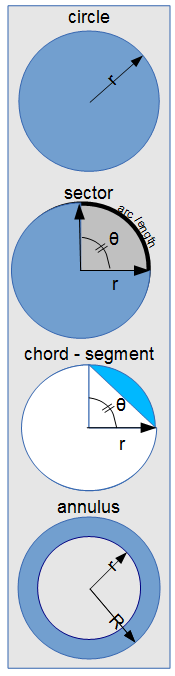 Circle Portions, ellipses, triangles, quadrilaterals and polygons including segments and sectors.
Circle Portions, ellipses, triangles, quadrilaterals and polygons including segments and sectors.
Description
The AREA and PERIMETER calculator provide equations to calculate the area and perimeters of different geometric shapes. The user chooses a shape and can enter the parameters in any of the various units provided by vCalc. The shapes include:
- circles
- ellipses
- triangles
- quadrilaterals
- polygons
Units
vCalc lets the user enter the dimensions of the area and perimeter formulas using any of the provided list of length units. These include a large number of metric, English and non-standard units (e.g. nautical miles and light years). vCalc's also enables the user to convert the answers to different units on-the-fly by selection on the pull-down menu.
Area
Area is the quantity that expresses the extent of a two-dimensional figure or shape, or planar lamina, in the plane. Surface area is its analog on the two-dimensional surface of a three-dimensional object. Area can be understood as the amount of material with a given thickness that would be necessary to fashion a model of the shape, or the amount of paint necessary to cover the surface with a single coat. It is the two-dimensional analog of the length of a curve (a one-dimensional concept) or the volume of a solid (a three-dimensional concept).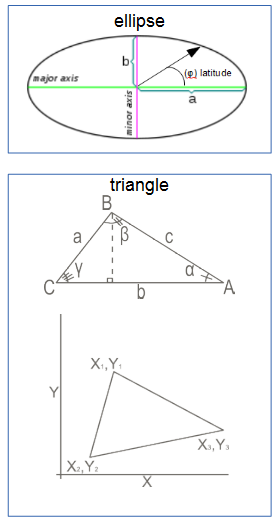 ellipse - triangle
ellipse - triangle
The area of a shape can be measured by comparing the shape to squares of a fixed size. In the International System of Units (SI), the standard unit of area is the square meter (written as m2), which is the area of a square whose sides are one meter long. A shape with an area of three square meters would have the same area as three such squares. In mathematics, the unit square is defined to have area one, and the area of any other shape or surface is a dimensionless real number.
There are several well-known formulas for the areas of simple shapes such as triangles, rectangles, and circles. Using these formulas, the area of any polygon can be found by dividing the polygon into triangles. For shapes with curved boundary, calculus is usually required to compute the area. Indeed, the problem of determining the area of plane figures was a major motivation for the historical development of calculus.
For a solid shape such as a sphere, cone, or cylinder, the area of its boundary surface is called the surface area. Formulas for the surface areas of simple shapes were computed by the ancient Greeks, but computing the surface area of a more complicated shape usually requires multivariable calculus.
Area plays an important role in modern mathematics. In addition to its obvious importance in geometry and calculus, area is related to the definition of determinants in linear algebra, and is a basic property of surfaces in differential geometry. In analysis, the area of a subset of the plane is defined using Lebesgue measure, though not every subset is measurable. In general, area in higher mathematics is seen as a special case of volume for two-dimensional regions. 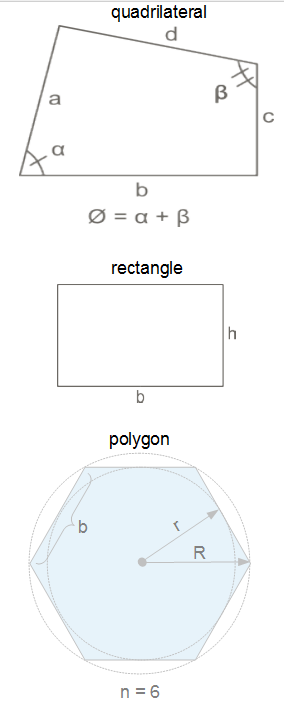 quadrilateral - polygon
quadrilateral - polygon
Area can be defined through the use of axioms, defining it as a function of a collection of certain plane figures to the set of real numbers. It can be proved that such a function exists.
Perimeter
A perimeter is a path that surrounds a two-dimensional shape. The word comes from the Greek peri (around) and meter (measure). The term may be used either for the path or its length - it can be thought of as the length of the outline of a shape. The perimeter of a circle or ellipse is called its circumference.
Calculating the perimeter has considerable practical applications. The perimeter can be used to calculate the length of fence required to surround a yard or garden. The perimeter of a wheel (its circumference) describes how far it will roll in one revolution. Similarly, the amount of string wound around a spool is related to the spool's perimeter.
Circumference of an Ellipse
The circumference 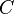 of an ellipse is:
of an ellipse is:
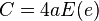
where again a is the length of the semi-major axis and e is the eccentricity and where the function 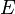 is the complete elliptic integral of the second kind (the arc length of an ellipse, in general, has no closed-form solution in terms of elementary functions and the elliptic integrals were motivated by this problem). This may be evaluated directly using the Carlson symmetric form. This gives a succinct and rapidly converging method for evaluating the circumference.
is the complete elliptic integral of the second kind (the arc length of an ellipse, in general, has no closed-form solution in terms of elementary functions and the elliptic integrals were motivated by this problem). This may be evaluated directly using the Carlson symmetric form. This gives a succinct and rapidly converging method for evaluating the circumference.
The exact infinite series is:
![C = 2\pi a \left[{1 - \left({1\over 2}\right)^2e^2 - \left({1\cdot 3\over 2\cdot 4}\right)^2{e^4\over 3} - \left({1\cdot 3\cdot 5\over 2\cdot 4\cdot 6}\right)^2{e^6\over5} - \cdots}\right]](https://www.vcalc.com/attachments/8effbb57-b087-11e4-a9fb-bc764e2038f2/e723fa65a4a183cc50621b7581e0c91d.png)
or
![C = 2\pi a \left[1 - \sum_{n=1}^\infty \left(\frac{(2n - 1)!!}{2^n n!}\right)^2 \frac{e^{2n}}{2n - 1}\right],](https://www.vcalc.com/attachments/8effbb57-b087-11e4-a9fb-bc764e2038f2/0a1f9b3824382486507885622ddcf283.png)
where 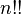 is the double factorial. Unfortunately, this series converges rather slowly; however, by expanding in terms of
is the double factorial. Unfortunately, this series converges rather slowly; however, by expanding in terms of 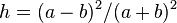 , Ivory and Bessel derived an expression which converges much more rapidly,
, Ivory and Bessel derived an expression which converges much more rapidly,
![C = \pi (a + b) \left[1 + \sum_{n=1}^\infty \left(\frac{(2n - 1)!!}{2^n n!}\right)^2 \frac{h^n}{(2n - 1)^2}\right].](https://www.vcalc.com/attachments/8effbb57-b087-11e4-a9fb-bc764e2038f2/b54c1b37bb00518dd1a42b4c6f85a17c.png)
Ramanujan gives two good approximations for the circumference in §16 of; they are
![C \approx \pi \left[3(a+b) - \sqrt{(3a+b)(a+3b)}\right]= \pi \left[3(a+b)-\sqrt{10ab+3(a^2+b^2)}\right]](https://www.vcalc.com/attachments/8effbb57-b087-11e4-a9fb-bc764e2038f2/98fe993c7427f52b03ef3a53a9d0b331.png)
and
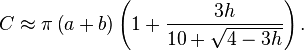
The errors in these approximations, which were "obtained empirically", are of order h3 and h5, respectively.
These approximations are in the calculator as apx1 and apx3. Note: the substitution for h has been made in the display.
History
Circle area
In the fifth century BCE, Hippocrates of Chios was the first to show that the area of a disk (the region enclosed by a circle) is proportional to the square of its diameter, as part of his quadrature of the lune of Hippocrates but did not identify the constant of proportionality. Eudoxus of Cnidus, also in the fifth century BCE, also found that the area of a disk is proportional to its radius squared.
Subsequently, Book I of Euclid's Elements dealt with equality of areas between two-dimensional figures. The mathematician Archimedes used the tools of Euclidean geometry to show that the area inside a circle is equal to that of a right triangle whose base has the length of the circle's circumference and whose height equals the circle's radius, in his book Measurement of a Circle. (The circumference is 2πr, and the area of a triangle is half the base times the height, yielding the area πr2 for the disk.) Archimedes approximated the value of π (and hence the area of a unit-radius circle) with his doubling method, in which he inscribed a regular triangle in a circle and noted its area, then doubled the number of sides to give a regular hexagon, then repeatedly doubled the number of sides as the polygon's area got closer and closer to that of the circle (and did the same with circumscribed polygons).
Swiss scientist Johann Heinrich Lambert in 1761 proved that π, the ratio of a circle's area to its squared radius, is irrational, meaning it is not equal to the quotient of any two whole numbers. French mathematician Adrien-Marie Legendre proved in 1794 that π2 is also irrational. In 1882, German mathematician Ferdinand von Lindemann proved that π is transcendental (not the solution of any polynomial equation with rational coefficients), confirming a conjecture made by both Legendre and Euler.
Triangle area
Heron (or Hero) of Alexandria found what is known as Heron's formula for the area of a triangle in terms of its sides, and a proof can be found in his book, Metrica, written around 60 CE. It has been suggested that Archimedes knew the formula over two centuries earlier, and since Metrica is a collection of the mathematical knowledge available in the ancient world, it is possible that the formula predates the reference given in that work.
In 499 Aryabhata, a great mathematician-astronomer from the classical age of Indian mathematics and Indian astronomy, expressed the area of a triangle as one-half the base times the height in the Aryabhatiya (section 2.6).
A formula equivalent to Heron's was discovered by the Chinese independently of the Greeks. It was published in 1247 in Shushu Jiuzhang (“Mathematical Treatise in Nine Sections”), written by Qin Jiushao.
Quadrilateral area
In the 600s CE, Brahmagupta developed a formula, now known as Brahmagupta's formula, for the area of a cyclic quadrilateral (a quadrilateral inscribed in a circle) in terms of its sides. In 1842 the German mathematicians Carl Anton Bretschneider and Karl Georg Christian von Staudt independently found a formula, known as Bretschneider's formula, for the area of any quadrilateral.
General polygon area
The development of Cartesian coordinates by René Descartes in the 1600s allowed the development of the surveyor's formula for the area of any polygon with known vertex locations by Gauss in the 1800s.
See Also
- Volume - Calculator with equations for calculating the volume of different shaped objects.
References
- Wikipedia - http://en.wikipedia.org/wiki/Area
- Wikipedia - http://en.wikipedia.org/wiki/Perimeter
- Wikipedia - http://en.wikipedia.org/wiki/Ellipse#Circumference