The Torispherical Head Volume and Height calculator computes the volume of an torispherical head based on the crown radius (R), knuckle radius (a) and the Diameter (D). It also computes the head height (h). 
INSTRUCTIONS: Choose units and enter the following:
- (R) Crown Radius
- (a) Knuckle Radius
- (D) Diameter of the head
Torispherical Head Volume (V) and Height (h): The volume is returned in cubic meters and the height is returned in meters. However, these can be automatically converted to compatible units via the pull-down menu.
Torispheric-head or Dished End Calculators
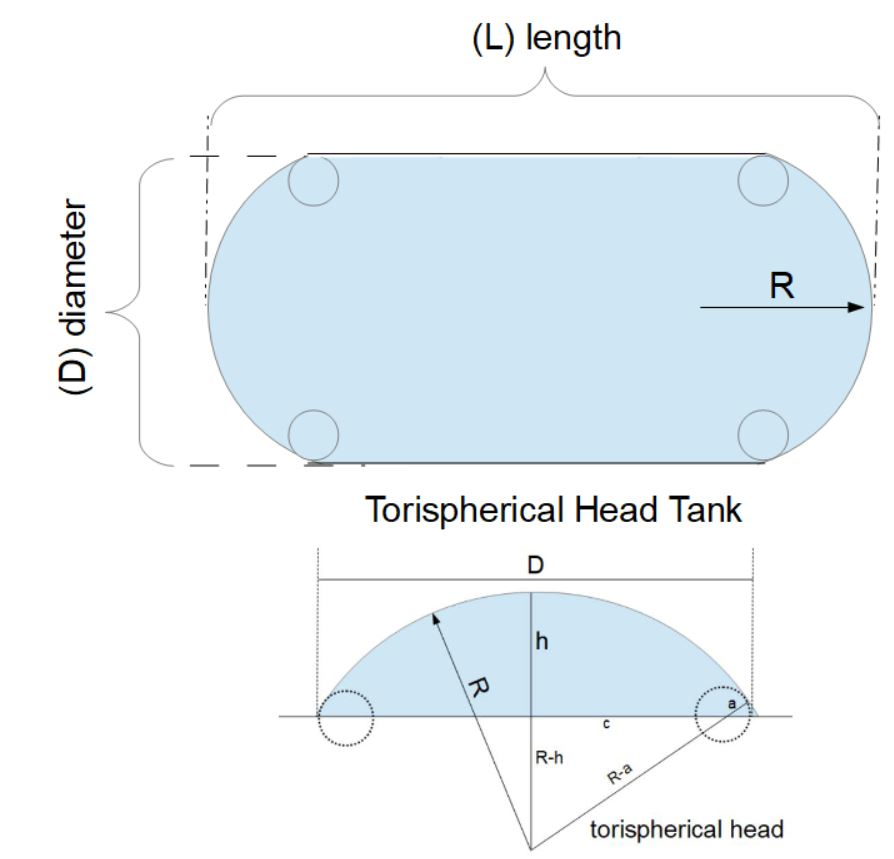Capacity of a Dished End Tank: Computes the volume of a cylindrical tank with torispherical heads based on the length and diameter of the tank and the crown radius and knuckle radius of the torispherical heads.- Torispherical Head Volume: CORRECTED. Computes the volume and diameter of an torispherical head (dish-head) based on the crown radius, knuckle radius and the height.
- Torispherical Head Volume and Height: computes the volume of an torispherical head based on the crown radius, knuckle radius and the Diameter. It also computes the head height.
- Volume of a Torispherical Head Cylindrical Tank: Computes the volume of a cylindrical tank with torispherical heads (dish end) based on the length and diameter of the tank and the crown radius and knuckle radius of the torispherical heads.
- Mass of the Contents of Torispherical Head Tank: Computes the weight / mass of the contents of tank with torispherical heads based on the volume and density of the contents.
The Math / Science
The formula for the volume of an Torispherical Head is as follows:
`V = π/3[2⋅h⋅R²-(2a² + c² + 2aR)(R-h)+3a²c sin‾¹( (R-h)/(R-a))]`
where:
- V is the volume of the Torispherical Head
- R is the crown radius
- h is the head height.
- a is the knuckle radius
The value of c is computed from R, h and a as follows:
`c = sqrt( (R-a)² - (R-h)² )`
solving for h:
`h = R - sqrt((R-a)^2 - c^2)`
We also know that:
D = 2(c+a)
which means that:
c = D/2 - a