28.5 The principle of least time for reflection by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

28.5 The principle of least time for reflection (optional)

We had to choose between an unwieldy explanation of reflection at the atomic level and a simpler geometric description that was not as fundamental. There is a third approach to describing the interaction of light and matter which is very deep and beautiful. Emphasized by the twentieth-century physicist Richard Feynman, it is called the principle of least time, or Fermat's principle.

Let's start with the motion of light that is not interacting with matter at all. In a vacuum, a light ray moves in a straight line. This can be rephrased as follows: of all the conceivable paths light could follow from `P` to `Q`, the only one that is physically possible is the path that takes the least time.

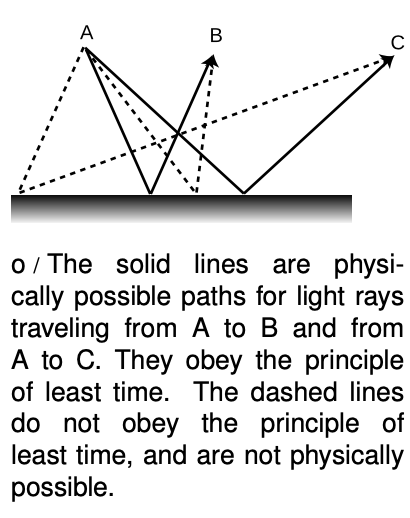
What about reflection? If light is going to go from one point to another, being reflected on the way, the quickest path is indeed the one with equal angles of incidence and reflection. If the starting and ending points are equally far from the reflecting surface, o, it's not hard to convince yourself that this is true, just based on symmetry. There is also a tricky and simple proof, shown in figure p, for the more general case where the points are at different distances from the surface.

Not only does the principle of least time work for light in a vacuum and light undergoing reflection, we will also see in a later chapter that it works for the bending of light when it passes from one medium into another.

Although it is beautiful that the entire ray model of light can be reduced to one simple rule, the principle of least time, it may seem a little spooky to speak as if the ray of light is intelligent, and has carefully planned ahead to find the shortest route to its destination. How does it know in advance where it's going? What if we moved the mirror while the light was en route, so conditions along its planned path were not what it “expected?” The answer is that the principle of least time is really a shortcut for finding certain results of the wave model of light, which is the topic of the last chapter of this book.

There are a couple of subtle points about the principle of least time. First, the path does not have to be the quickest of all possible paths; it only needs to be quicker than any path that differs infinitesimally from it. In figure p, for instance, light could get from `A` to `B` either by the reflected path AQB or simply by going straight from `A` to `B`. Although `AQB` is not the shortest possible path, it cannot be shortened by changing it infinitesimally, e.g., by moving `Q` a little to the right or left. On the other hand, path `APB` is physically impossible, because it is possible to improve on it by moving point `P` infinitesimally to the right.

It's not quite right to call this the principle of least time. In figure q, for example, the four physically possible paths by which a ray can return to the center consist of two shortest-time paths and two longest-time paths. Strictly speaking, we should refer to the principle of least or greatest time, but most physicists omit the niceties, and assume that other physicists understand that both maxima and minima are possible.

28.5 The principle of least time for reflection by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.