10.2 Newton's law of gravity by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
10.2 Newton's law of gravity
The sun's force on the planets obeys an inverse square law.
Kepler's laws were a beautifully simple explanation of what the planets did, but they didn't address why they moved as they did. Did the sun exert a force that pulled a planet toward the center of its orbit, or, as suggested by Descartes, were the planets circulating in a whirlpool of some unknown liquid? Kepler, working in the Aristotelian tradition, hypothesized not just an inward force exerted by the sun on the planet, but also a second force in the direction of motion to keep the planet from slowing down. Some speculated that the sun attracted the planets magnetically.
Once Newton had formulated his laws of motion and taught them to some of his friends, they began trying to connect them to Kepler's laws. It was clear now that an inward force would be needed to bend the planets' paths. This force was presumably an attraction between the sun and each planet. (Although the sun does accelerate in response to the  attractions of the planets, its mass is so great that the effect had never been detected by the prenewtonian astronomers.) Since the outer planets were moving slowly along more gently curving paths than the inner planets, their accelerations were apparently less. This could be explained if the sun's force was determined by distance, becoming weaker for the farther planets. Physicists were also familiar with the noncontact forces of electricity and magnetism, and knew that they fell off rapidly with distance, so this made sense.
attractions of the planets, its mass is so great that the effect had never been detected by the prenewtonian astronomers.) Since the outer planets were moving slowly along more gently curving paths than the inner planets, their accelerations were apparently less. This could be explained if the sun's force was determined by distance, becoming weaker for the farther planets. Physicists were also familiar with the noncontact forces of electricity and magnetism, and knew that they fell off rapidly with distance, so this made sense.
In the approximation of a circular orbit, the magnitude of the sun's force on the planet would have to be
[1] `F=ma` = `mv^2"/"r`.
Now although this equation has the magnitude, `v`, of the velocity vector in it, what Newton expected was that there would be a more fundamental underlying equation for the force of the sun on a planet, and that that equation would involve the distance,`r`, from the sun to the object, but not the object's speed, `v` --- motion doesn't make objects lighter or heavier.
self-check:
If eq. [1] really was generally applicable, what would happen to an object released at rest in some empty region of the solar system?
Equation [1] was thus a useful piece of information which could be related to the data on the planets simply because the planets happened to be going in nearly circular orbits, but Newton wanted to combine it with other equations and eliminate `v` algebraically in order to find a deeper truth.
To eliminate `v`, Newton used the equation
[2] `v="circumference"/T=(2pir)/T`.
Of course this equation would also only be valid for planets in nearly circular orbits. Plugging this into eq. [1] to eliminate `v` gives
[3] `F=(4pi^2mr)/T^2`.
 This unfortunately has the side-effect of bringing in the period, `T`, which we expect on similar physical grounds will not occur in the final answer. That's where the circular-orbit case, `Tpropr^(3/2)`, of Kepler's law of periods comes in. Using it to eliminate `T` gives a result that depends only on the mass of the planet and its distance from the sun:
This unfortunately has the side-effect of bringing in the period, `T`, which we expect on similar physical grounds will not occur in the final answer. That's where the circular-orbit case, `Tpropr^(3/2)`, of Kepler's law of periods comes in. Using it to eliminate `T` gives a result that depends only on the mass of the planet and its distance from the sun:
`F\propto m"/"r^2`. [force of the sun on a planet of mass `m` at a distance `r` from the sun; same proportionality constant for all the planets]
(Since Kepler's law of periods is only a proportionality, the final result is a proportionality rather than an equation, so there is no point in hanging on to the factor of `4pi^2`.)
As an example, the “twin planets” Uranus and Neptune have nearly the same mass, but Neptune is about twice as far from the sun as Uranus, so the sun's gravitational force on Neptune is about four times smaller.
self-check:
Fill in the steps leading from equation [3] to `Fpropm"/"r^2`.
(answer in the back of the PDF version of the book)
The forces between heavenly bodies are the same type of force as terrestrial gravity.
OK, but what kind of force was it? It probably wasn't magnetic, since magnetic forces have nothing to do with mass. Then came Newton's great insight. Lying under an apple tree and looking up at the moon in the sky, he saw an apple fall. Might not the earth also attract the moon with the same kind of gravitational force? The moon orbits the earth in the same way that the planets orbit the sun, so maybe the earth's force on the falling apple, the earth's force on the moon, and the sun's force on a planet were all the same type of force.
There was an easy way to test this hypothesis numerically. If it was true, then we would expect the gravitational forces exerted by the earth to follow the same `Fpropm"/"r^2` rule as the forces exerted by the sun, but with a different constant of proportionality appropriate to the earth's gravitational strength. The issue arises now of how to define the distance, `r`, between the earth and the apple. An apple in England is closer to some parts of the earth than to others, but suppose we take `r` to be the distance from the center of the earth to the apple, i.e., the radius of the earth. (The issue of how to measure `r` did not arise in the analysis of the planets' motions because the sun and planets are so small compared to the distances separating them.) Calling the proportionality constant `k`, we have
`F_"earth on apple"=km_"apple""/"r_"earth"^2`
`F_"earth on moon"=km_"moon""/"d_"earth-moon"^2`.
Newton's second law says `a=F"/"m`, so
`a_"apple"=k"/"r_"earth"^2`
`a_"moon"=k"/"d_"earth-moon"^2`.
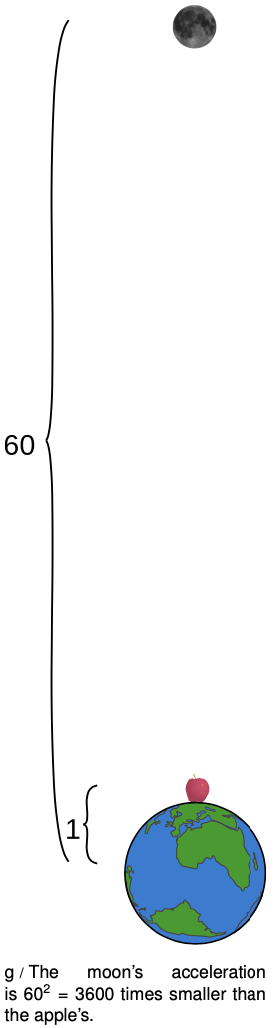
The Greek astronomer Hipparchus had already found 2000 years before that the distance from the earth to the moon was about 60 times the radius of the earth, so if Newton's hypothesis was right, the acceleration of the moon would have to be `60^2=3600` times less than the acceleration of the falling apple.
Applying `a=v^2"/"r` to the acceleration of the moon yielded an acceleration that was indeed 3600 times smaller than `9.8 m"/"s^2`, and Newton was convinced he had unlocked the secret of the mysterious force that kept the moon and planets in their orbits.
Newton's law of gravity
The proportionality `Fpropm"/"r^2` for the gravitational force on an object of mass `m` only has a consistent proportionality constant for various objects if they are being acted on by the gravity of the same object. Clearly the sun's gravitational strength is far greater than the earth's, since the planets all orbit the sun and do not exhibit any very large accelerations caused by the earth (or by one another). What property of the sun gives it its great gravitational strength? Its great volume? Its great mass? Its great temperature? Newton reasoned that if the force was proportional to the mass of the object being acted on, then it would also make sense if the determining factor in the gravitational strength of the object exerting the force was its own mass. Assuming there were no other factors affecting the gravitational force, then the only other thing needed to make quantitative predictions of gravitational forces would be a proportionality constant. Newton called that proportionality constant `G`, so here is the complete form of the law of gravity he hypothesized.[gravitational force between objects of mass m1 and m2, separated by a distance r; r is not the radius of anything ]
Newton conceived of gravity as an attraction between any two masses in the universe. The constant `G` tells us how many newtons the attractive force is for two 1-kg masses separated by a distance of 1 m. The experimental determination of `G` in ordinary units (as opposed to the special, nonmetric, units used in astronomy) is described in section 10.5. This difficult measurement was not accomplished until long after Newton's death.
Example 1: The units of `G`
`=>` What are the units of `G`?
`=>` Solving for `G` in Newton's law of gravity gives
`G=(Fr^2)/(m_1m_2)`,
so the units of `G` must be `Ncdotm^2"/"kg^2`. Fully adorned with units, the value of `G` is `6.67×10^(-11) N?m^2"/"kg^2`.
Example 2: Newton's third law
`=>` Is Newton's law of gravity consistent with Newton's third law?
`=>` The third law requires two things. First, `m_1`'s force on `m_2` should be the same as `m_2`'s force on `m_1`. This works out, because the product `m_1m_2` gives the same result if we interchange the labels 1 and 2. Second, the forces should be in opposite directions. This condition is also satisfied, because Newton's law of gravity refers to an attraction: each mass pulls the other toward itself.
Example 3: Pluto and Charon
`=>` Pluto's moon Charon is unusually large considering Pluto's size, giving them the character of a double planet. Their masses are `1.25×10^22` and `1.9×10^21` kg, and their average distance from one another is `1.96×10^4` km. What is the gravitational force between them?
`=>` If we want to use the value of `G` expressed in SI (meter-kilogram-second) units, we first have to convert the distance to `1.96×10^7` m. The force is
`((6.67×10^(-11) Ncdotm^2"/"kg^2)(1.25×10^22 kg)(1.9×10^21 kg))/(1.96×10^7 m)^2=4.1×10^18 N`
 The proportionality to `1"/"r^2` are found in many other phenomena in which some effect spreads out from a point. For instance, the intensity of the light from a candle is proportional to `1"/"r^2`, because at a distance `r` from the candle, the light has to be spread out over the surface of an imaginary sphere of area `4pir^2` . The same is true for the intensity of sound from a firecracker, or the intensity of gamma radiation emitted by the Chernobyl reactor. It's important, however, to realize that this is only an analogy. Force does not travel through space as sound or light does, and force is not a substance that can be spread thicker or thinner like butter on toast.
The proportionality to `1"/"r^2` are found in many other phenomena in which some effect spreads out from a point. For instance, the intensity of the light from a candle is proportional to `1"/"r^2`, because at a distance `r` from the candle, the light has to be spread out over the surface of an imaginary sphere of area `4pir^2` . The same is true for the intensity of sound from a firecracker, or the intensity of gamma radiation emitted by the Chernobyl reactor. It's important, however, to realize that this is only an analogy. Force does not travel through space as sound or light does, and force is not a substance that can be spread thicker or thinner like butter on toast.
Although several of Newton's contemporaries had speculated that the force of gravity might be proportional to `1"/"r^2`, none of them, even the ones who had learned Newton's laws of motion, had had any luck proving that the resulting orbits would be ellipses, as Kepler had found empirically. Newton did succeed in proving that elliptical orbits would result from a `1"/"r^2` force, but we postpone the proof until the chapter 15 because it can be accomplished much more easily using the concepts of energy and angular momentum.
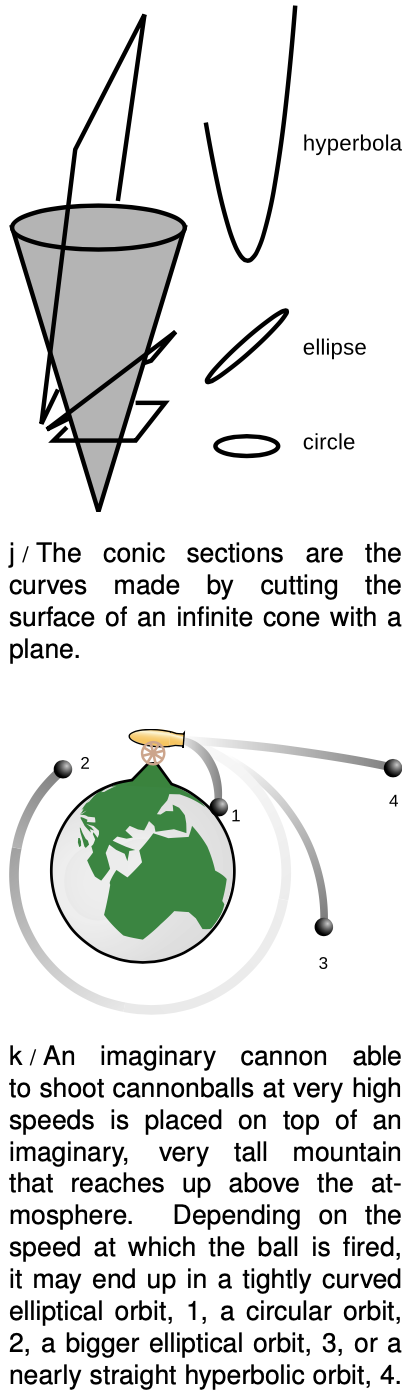
Newton also predicted that orbits in the shape of hyperbolas should be possible, and he was right. Some comets, for instance, orbit the sun in very elongated ellipses, but others pass through the solar system on hyperbolic paths, never to return. Just as the trajectory of a faster baseball pitch is flatter than that of a more slowly thrown ball, so the curvature of a planet's orbit depends on its speed. A spacecraft can be launched at relatively low speed, resulting in a circular orbit about the earth, or it can be launched at a higher speed, giving a more gently curved ellipse that reaches farther from the earth, or it can be launched at a very high speed which puts it in an even less curved hyperbolic orbit. As you go very far out on a hyperbola, it approaches a straight line, i.e., its curvature eventually becomes nearly zero.
Newton also was able to prove that Kepler's second law (sweeping out equal areas in equal time intervals) was a logical consequence of his law of gravity. Newton's version of the proof is moderately complicated, but the proof becomes trivial once you understand the concept of angular momentum, which will be covered later in the course. The proof will therefore be deferred until section 15.7.
self-check:
Which of Kepler's laws would it make sense to apply to hyperbolic orbits?
(answer in the back of the PDF version of the book)
`=>` Solved problem: Visiting Ceres — problem 10
`=>` Solved problem: Geosynchronous orbit — problem 16
`=>` Solved problem: Why `a` equals `g` — problem 11
`=>` Solved problem: Ida and Dactyl — problem 12
`=>` Solved problem: Another solar system — problem 15
`=>` Solved problem: Weight loss — problem 19
`=>` Solved problem: The receding moon — problem 17
Discussion Questions
`mathbf"A"` How could Newton find the speed of the moon to plug in to `a=v^2"/"r`?
`mathbf"B"` Two projectiles of different mass shot out of guns on the surface of the earth at the same speed and angle will follow the same trajectories, assuming that air friction is negligible. (You can verify this by throwing two objects together from your hand and seeing if they separate or stay side by side.) What corresponding fact would be true for satellites of the earth having different masses?
`mathbf"C"` What is wrong with the following statement? “A comet in an elliptical orbit speeds up as it approaches the sun, because the sun's force on it is increasing.”
`mathbf"D"` Why would it not make sense to expect the earth's gravitational force on a bowling ball to be inversely proportional to the square of the distance between their surfaces rather than their centers?
`mathbf"E"` Does the earth accelerate as a result of the moon's gravitational force on it? Suppose two planets were bound to each other gravitationally the way the earth and moon are, but the two planets had equal masses. What would their motion be like?
`mathbf"F"` Spacecraft normally operate by firing their engines only for a few minutes at a time, and an interplanetary probe will spend months or years on its way to its destination without thrust. Suppose a spacecraft is in a circular orbit around Mars, and it then briefly fires its engines in reverse, causing a sudden decrease in speed. What will this do to its orbit? What about a forward thrust?
10.2 Newton's law of gravity by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
