10.1 Kepler's laws by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
10.1 Kepler's laws
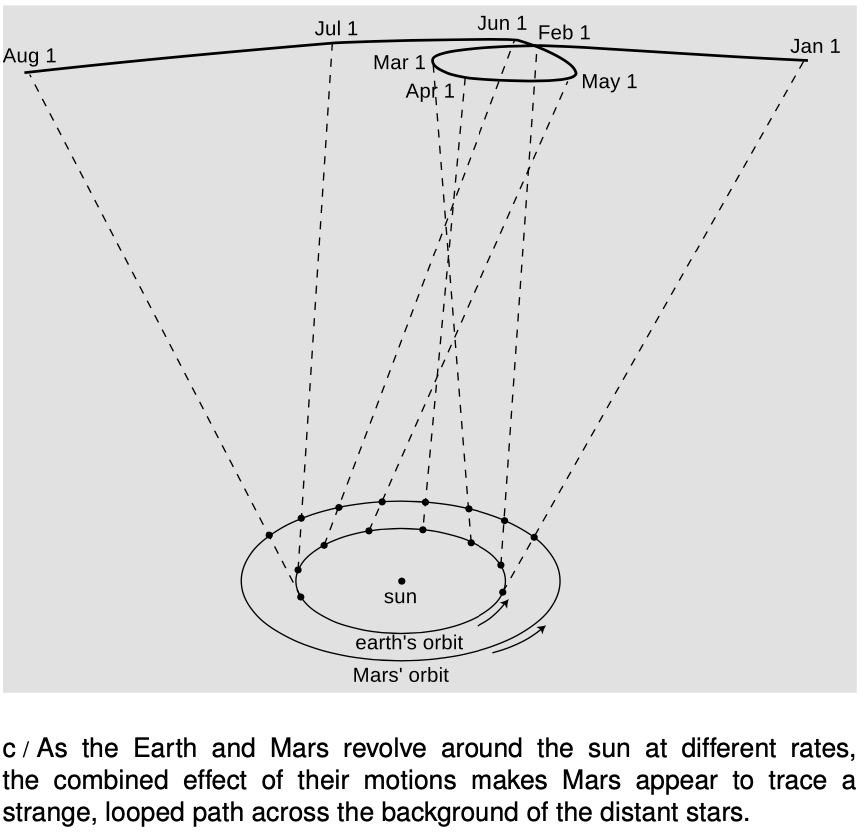
Newton wouldn't have been able to figure out why the planets move the way they do if it hadn't been for the astronomer Tycho Brahe (1546-1601) and his protege Johannes Kepler (1571-1630), who together came up with the first simple and accurate description of how the planets actually do move. The difficulty of their task is suggested by figure c, which shows how the relatively simple orbital motions of the earth and Mars combine so that as seen from earth Mars appears to be staggering in loops like a drunken sailor.
Brahe, the last of the great naked-eye astronomers, collected extensive data on the motions of the planets over a period of many years, taking the giant step from the previous observations' accuracy of about 10 minutes of arc (10/60 of a degree) to an unprecedented 1 minute. The quality of his work is all the more remarkable considering that his observatory consisted of four giant brass protractors mounted upright in his castle in Denmark. Four different observers would simultaneously measure the position of a planet in order to check for mistakes and reduce random errors.
With Brahe's death, it fell to his former assistant Kepler to try to make some sense out of the volumes of data. Kepler, in contradiction to his late boss, had formed a prejudice, a correct one as it turned out, in favor of the theory that the earth and planets revolved around the sun, rather than the earth staying fixed and everything rotating about it. Although motion is relative, it is not just a matter of opinion what circles what. The earth's rotation and revolution about the sun make it a noninertial reference frame, which causes detectable violations of Newton's laws when one attempts to describe sufficiently precise experiments in the earth-fixed frame. Although such direct experiments were not carried out until the 19th century, what convinced everyone of the sun-centered system in the 17th century was that Kepler was able to come up with a surprisingly simple set of mathematical and geometrical rules for describing the planets' motion using the sun-centered assumption. After 900 pages of calculations and many false starts and dead-end ideas, Kepler finally synthesized the data into the following three laws:
Kepler's elliptical orbit law
The planets orbit the sun in elliptical orbits with the sun at one focus.
Kepler's equal-area law
The line connecting a planet to the sun sweeps out equal areas in equal amounts of time.
Kepler's law of periods
The time required for a planet to orbit the sun, called its period, is proportional to the long axis of the ellipse raised to the 3/2 power. The constant of proportionality is the same for all the planets.
Although the planets' orbits are ellipses rather than circles, most are very close to being circular. The earth's orbit, for instance, is only flattened by 1.7% relative to a circle. In the special case of a planet in a circular orbit, the two foci (plural of “focus”) coincide at the center of the circle, and Kepler's elliptical orbit law thus says that the circle is centered on the sun. The equal-area law implies that a planet in a circular orbit moves around the sun with constant speed. For a circular orbit, the law of periods then amounts to a statement that the time for one orbit is proportional to `r^(3"/"2)`, where `r` is the radius. If all the planets were moving in their orbits at the same speed, then the time for one orbit would simply depend on the circumference of the circle, so it would only be proportional to `r` to the first power. The more drastic dependence on `r^(3"/"2)` means that the outer planets must be moving more slowly than the inner planets.
10.1 Kepler's laws by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.