24.2 Calculating magnetic fields and forces by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
24.2 Calculating magnetic fields and forces
Magnetostatics
Our study of the electric field built on our previous understanding of electric forces, which was ultimately based on Coulomb's law for the electric force between two point charges. Since magnetism is ultimately an interaction between currents, i.e., between moving charges, it is reasonable to wish for a magnetic analog of Coulomb's law, an equation that would tell us the magnetic force between any two moving point charges.
Such a law, unfortunately, does not exist. Coulomb's law describes the special case of electrostatics: if a set of charges is sitting around and not moving, it tells us the interactions among them. Coulomb's law fails if the charges are in motion, since it does not incorporate any allowance for the time delay in the outward propagation of a change in the locations of the charges.
A pair of moving point charges will certainly exert magnetic forces on one another, but their magnetic fields are like the v-shaped bow waves left by boats. Each point charge experiences a magnetic field that originated from the other charge when it was at some previous position. There is no way to construct a force law that tells us the force between them based only on their current positions in space.
There is, however, a science of magnetostatics that covers a great many important cases. Magnetostatics describes magnetic forces among currents in the special case where the currents are steady and continuous, leading to magnetic fields throughout space that do not change over time.
The magnetic field of a long, straight wire is one example that we can say something about without resorting to fancy mathematics. We saw in examples 4 on p. 627 and 14 on p. 639 that the electric field of a uniform line of charge is `E=(2kq)/(Lr)`, where `r` is the distance from the line and `q"/"L` is the charge per unit length. In a frame of reference moving at velocity `v` parallel to the line, this electric field will be observed as a combination of electric and magnetic fields. It therefore follows that the magnetic field of a long, straight, current-carrying wire must be proportional to `1"/"r`. We also expect that it will be proportional to the Coulomb constant, which sets the strength of electric and magnetic interactions, and to the current `I` in the wire. The complete expression turns out to be `B=k/c^2*(2I)/r`. This is identical to the expression for `E` except for replacement of `q"/"L` with `I` and an additional factor of `1"/"c^2`. The latter occurs because magnetism is a purely relativistic effect, and the relativistic length contraction depends on `v^2"/"c^2`.
Figure f shows the equations for some of the more commonly encountered configurations, with illustrations of their field patterns. They all have a factor of `k"/"c^2` in front, which shows that magnetism is just electricity (`k`) seen through the lens of relativity (`1"/"c^2`). A convenient feature of SI units is that `k"/"c^2` has a numerical value of exactly `10^(-7)`, with units of `N"/"A^2`.
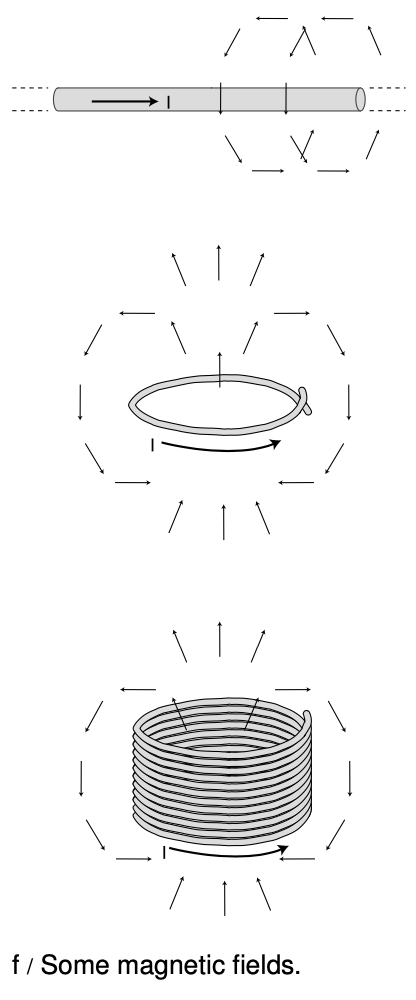Field created by a long, straight wire carrying current `I`:
Here `r` is the distance from the center of the wire. The field vectors trace circles in planes perpendicular to the wire, going clockwise when viewed from along the direction of the current.
Field created by a single circular loop of current:
The field vectors form a dipole-like pattern, coming through the loop and back around on the outside. Each oval path traced out by the field vectors appears clockwise if viewed from along the direction the current is going when it punches through it. There is no simple equation for a field at an arbitrary point in space, but for a point lying along the central axis perpendicular to the loop, the field is
`B=k/c^2 2piIb^2(b^2+z^2)^(-3/2)`,
where `b` is the radius of the loop and `z` is the distance of the point from the plane of the loop.
Field created by a solenoid (cylindrical coil):
The field pattern is similar to that of a single loop, but for a long solenoid the paths of the field vectors become very straight on the inside of the coil and on the outside immediately next to the coil. For a sufficiently long solenoid, the interior field also becomes very nearly uniform, with a magnitude of
where `N` is the number of turns of wire and `?` is the length of the solenoid. The field near the mouths or outside the coil is not constant, and is more difficult to calculate. For a long solenoid, the exterior field is much smaller than the interior field.
Don't memorize the equations!
Force on a charge moving through a magnetic field
We now know how to calculate magnetic fields in some typical situations, but one might also like to be able to calculate magnetic forces, such as the force of a solenoid on a moving charged particle, or the force between two parallel current-carrying wires.
We will restrict ourselves to the case of the force on a charged particle moving through a magnetic field, which allows us to calculate the force between two objects when one is a moving charged particle and the other is one whose magnetic field we know how to find. An example is the use of solenoids inside a TV tube to guide the electron beam as it paints a picture.
Experiments show that the magnetic force on a moving charged particle has a magnitude given by
where `v` is the velocity vector of the particle, and `theta` is the angle between the `v` and `B` vectors. Unlike electric and gravitational forces, magnetic forces do not lie along the same line as the field vector. The force is always perpendicular to both `v` and `B`. Given two vectors, there is only one line perpendicular to both of them, so the force vector points in one of the two possible directions along this line. For a positively charged particle, the direction of the force vector can be found as follows. First, position the `v` and `B` vectors with their tails together. The direction of `F` is such that if you sight along it, the `B` vector is clockwise from the `v` vector; for a negatively charged particle the direction of the force is reversed. Note that since the force is perpendicular to the particle's motion, the magnetic field never does work on it.
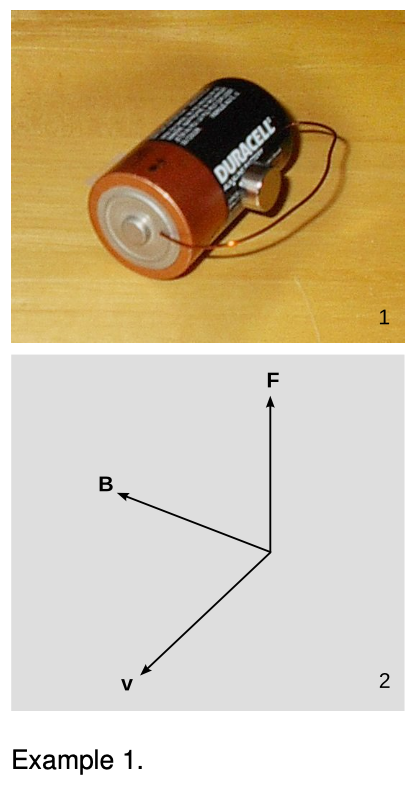Example 1: Magnetic levitation
In figure 24.2.2, a small, disk-shaped permanent magnet is stuck on the side of a battery, and a wire is clasped loosely around the battery, shorting it. A large current flows through the wire. The electrons moving through the wire feel a force from the magnetic field made by the permanent magnet, and this force levitates the wire.
From the photo, it's possible to find the direction of the magnetic field made by the permanent magnet. The electrons in the copper wire are negatively charged, so they flow from the negative (flat) terminal of the battery to the positive terminal (the one with the bump, in front). As the electrons pass by the permanent magnet, we can imagine that they would experience a field either toward the magnet, or away from it, depending on which way the magnet was flipped when it was stuck onto the battery. Imagine sighting along the upward force vector, which you could do if you were a tiny bug lying on your back underneath the wire. Since the electrons are negatively charged, the `B` vector must be counterclockwise from the `v` vector, which means toward the magnet.
Example 2: A circular orbit
Magnetic forces cause a beam of electrons to move in a circle. The beam is 
created in a vacuum tube, in which a small amount of hydrogen gas has been left. A few of the electrons strike hydrogen molecules, creating light and letting us see the beam. A magnetic field is produced by passing a current (meter) through the circular coils of wire in front of and behind the tube. In the bottom figure, with the magnetic field turned on, the force perpendicular to the electrons' direction of motion causes them to move in a circle.
Example 3: Nervous-system effects during an MRI scan
During an MRI scan of the head, the patient's nervous system is exposed to intense magnetic fields, and there are ions moving around in the nerves. The resulting forces on the ions can cause symptoms such as vertigo.
Energy in the magnetic field
On p. 631 I gave equations for the energy stored in the gravitational and electric fields. Since a magnetic field is essentially an electric field seen in a different frame of reference, we expect the magnetic-field equation to be closely analogous to the electric version, and it is:
(energy stored in the gravitational field per `m^3`): `-(1/8piG)|g|^2`
(energy stored in the electric field per `m^3`): `(1/8pik)|E|^2`
(energy stored in the magnetic field per `m^3`): `=c^2/(8pik)|B|^2`
The idea here is that `k"/"c^2` is the magnetic version of the electric quantity `k`, the `1"/"c^2` representing the fact that magnetism is a relativistic effect.
Example 4: Getting killed by a solenoid
Solenoids are very common electrical devices, but they can be a hazard to someone who is working on them. Imagine a solenoid that initially has a DC current passing through it. The current creates a magnetic field inside and around it, which contains energy. Now suppose that we break the circuit. Since there is no longer a complete circuit, current will quickly stop flowing, and the magnetic field will collapse very quickly. The field had energy stored in it, and even a small amount of energy can create a dangerous power surge if released over a short enough time interval. It is prudent not to fiddle with a solenoid that has current flowing through it, since breaking the circuit could be hazardous to your health.
As a typical numerical estimate, let's assume a `40 cm × 40 cm ×40 cm` solenoid with an interior magnetic field of `1.0` T (quite a strong field). For the sake of this rough estimate, we ignore the exterior field, which is weak, and assume that the solenoid is cubical in shape. The energy stored in the field is
(energy per unit volume)(volume)`=c^2/(8pik)|B|^2V`
`=3×10^4 J`
That's a lot of energy!
24.2 Calculating magnetic fields and forces by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.