18.5 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
damping — the dissipation of a vibration's energy into heat energy, or the frictional force that causes the loss of energy
quality factor — the number of oscillations required for a system's energy to fall off by a factor of 535 due to damping
driving force — an external force that pumps energy into a vibrating system
resonance — the tendency of a vibrating system to respond most strongly to a driving force whose frequency is close to its own natural frequency of vibration
steady state — the behavior of a vibrating system after it has had plenty of time to settle into a steady response to a driving force
Notation
`Q` — the quality factor
`f_o` the natural (resonant) frequency of a vibrating system, i.e., the frequency at which it would vibrate if it was simply kicked and left alone}
`f `— the frequency at which the system actually vibrates, which in the case of a driven system is equal to the frequency of the driving force, not the natural frequency
Summary
The energy of a vibration is always proportional to the square of the amplitude, assuming the amplitude is small. Energy is lost from a vibrating system for various reasons such as the conversion to heat via friction or the emission of sound. This effect, called damping, will cause the vibrations to decay exponentially unless energy is pumped into the system to replace the loss. A driving force that pumps energy into the system may drive the system at its own natural frequency or at some other frequency. When a vibrating system is driven by an external force, we are usually interested in its steady-state behavior, i.e., its behavior after it has had time to settle into a steady response to a driving force. In the steady state, the same amount of energy is pumped into the system during each cycle as is lost to damping during the same period.
The following are four important facts about a vibrating system being driven by an external force:
(1) The steady-state response to a sinusoidal driving force occurs at the frequency of the force, not at the system's own natural frequency of vibration.
(2) A vibrating system resonates at its own natural frequency. That is, the amplitude of the steady-state response is greatest in proportion to the amount of driving force when the driving force matches the natural frequency of vibration.
(3) When a system is driven at resonance, the steady-state vibrations have an amplitude that is proportional to `Q`.
(4) The `FWHM` of a resonance is related to its `Q` and its resonant frequency `f_o` by the equation
`FWHM=f_o/Q`.
(This equation is only a good approximation when `Q` is large.)
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem
1.If one stereo system is capable of producing 20 watts of sound power and another can put out 50 watts, how many times greater is the amplitude of the sound wave that can be created by the more powerful system? (Assume they are playing the same music.)
2. Many fish have an organ known as a swim bladder, an air-filled cavity whose main purpose is to control the fish's buoyancy an allow it to keep from rising or sinking without having to use its muscles. In some fish, however, the swim bladder (or a small extension of it) is linked to the ear and serves the additional purpose of amplifying sound waves. For a typical fish having such an anatomy, the bladder has a resonant frequency of 300 Hz, the bladder's `Q` is 3, and the maximum amplification is about a factor of 100 in energy. Over what range of frequencies would the amplification be at least a factor of 50?
3. As noted in section 18.4, it is only approximately true that the amplitude has its maximum at the natural frequency `(1"/"2pi)sqrt(k"/"m)`. Being more careful, we should actually define two different symbols, `f_o=(1"/"2pi)sqrt(k"/"m)` and `f_(res)` for the slightly different frequency at which the amplitude is a maximum, i.e., the actual resonant frequency. In this notation, the amplitude as a function of frequency is
`A=F/(2pisqrt(4pi^2m^2(f^2-f_0^2)^2+b^2f^2))`.
Show that the maximum occurs not at `f_o` but rather at
`f_(res)=sqrt(f_0^2-b^2/(8pi^2m^2))=sqrt(f_0^2-1/2FWHM^2)`
Hint: Finding the frequency that minimizes the quantity inside the square root is equivalent to, but much easier than, finding the frequency that maximizes the amplitude. `int`
4. (a) Let `W` be the amount of work done by friction in the first cycle of oscillation, i.e., the amount of energy lost to heat. Find the fraction of the original energy `E` that remains in the oscillations after `n` cycles of motion.
(b) From this, prove the equation
`(1-W/E)^Q`=`e^(-2pi)`
(recalling that the number 535 in the definition of `Q` is `e^(2pi)`.
(c) Use this to prove the approximation `1"/"Qapprox(1"/"2pi)W"/"E`. (Hint: Use the approximation `ln(1+x)approxx`, which is valid for small values of `x`.)
5. The goal of this problem is to refine the proportionality `FWHMalphaf_(res)"/"Q` into the equation `FWHM=f_(res)"/"Q`, i.e., to prove that the constant of proportionality equals 1.
(a) Show that the work done by a damping force `F=-bv` over one cycle of steady-state motion equals `W_(damp)=-2pi^2bfA^2`. Hint: It is less confusing to calculate the work done over half a cycle, from `x=-A` to `x=+A`, and then double it.
(b) Show that the fraction of the undriven oscillator's energy lost to damping over one cycle is `|W_(damp)|"/"E=4pi^2bf`/`k`.
(c) Use the previous result, combined with the result of problem 4, to prove that `Q` equals `k"/"2pibf` .
(d) Combine the preceding result for `Q` with the equation `FWHM=b"/"2pim` from section 18.4 to prove the equation `FWHM=f_(res)"/"Q`. `int` `***`
6. (a) We observe that the amplitude of a certain free oscillation decreases from `A_o` to `A_o`/`Z` after `n` oscillations. Find its `Q`.`sqrt`
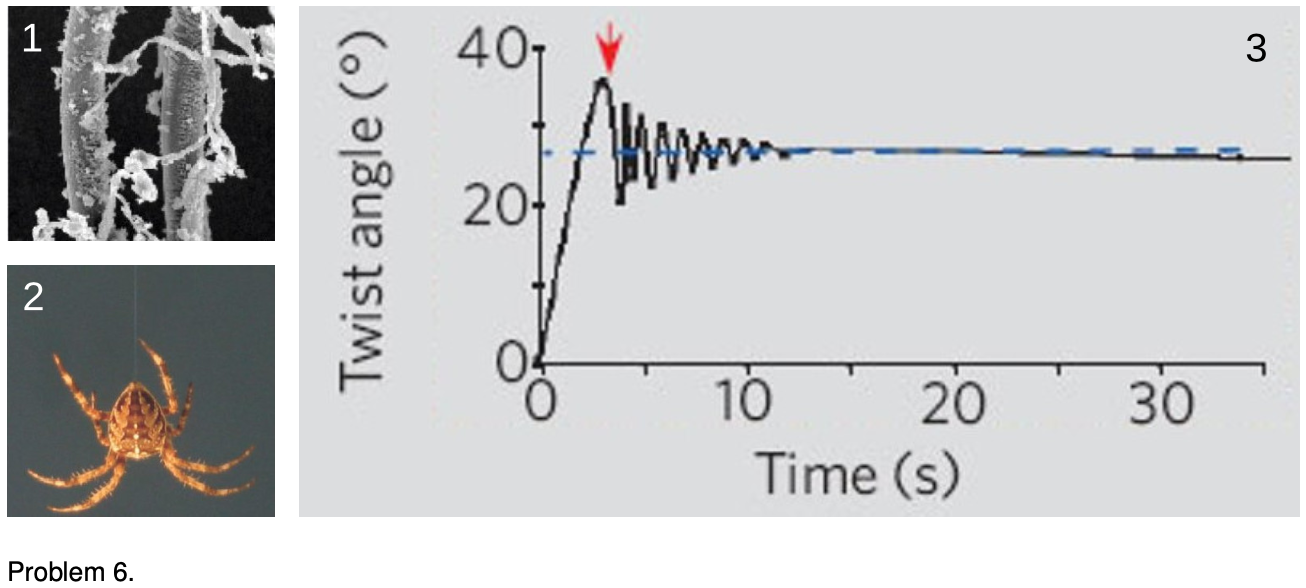
(b) The figure is from Shape memory in Spider draglines, Emile, Le Floch, and Vollrath, Nature 440:621 (2006). Panel 1 shows an electron microscope's image of a thread of spider silk. In 2, a spider is hanging from such a thread. From an evolutionary point of view, it's probably a bad thing for the spider if it twists back and forth while hanging like this. (We're referring to a back-and-forth rotation about the axis of the thread, not a swinging motion like a pendulum.) The authors speculate that such a vibration could make the spider easier for predators to see, and it also seems to me that it would be a bad thing just because the spider wouldn't be able to control its orientation and do what it was trying to do. Panel 3 shows a graph of such an oscillation, which the authors measured using a video camera and a computer, with a 0.1 g mass hung from it in place of a spider. Compared to human-made fibers such as kevlar or copper wire, the spider thread has an unusual set of properties:
- It has a low `Q`, so the vibrations damp out quickly.
- It doesn't become brittle with repeated twisting as a copper wire would.
- When twisted, it tends to settle in to a new equilibrium angle, rather than insisting on returning to its original angle. You can see this in panel 2, because although the experimenters initially twisted the wire by 35 degrees, the thread only performed oscillations with an amplitude much smaller than`±35` degrees, settling down to a new equilibrium at 27 degrees.
- Over much longer time scales (hours), the thread eventually resets itself to its original equilbrium angle (shown as zero degrees on the graph). (The graph reproduced here only shows the motion over a much shorter time scale.) Some human-made materials have this “memory” property as well, but they typically need to be heated in order to make them go back to their original shapes.
Focusing on property number 1, estimate the `Q` of spider silk from the graph. `sqrt`
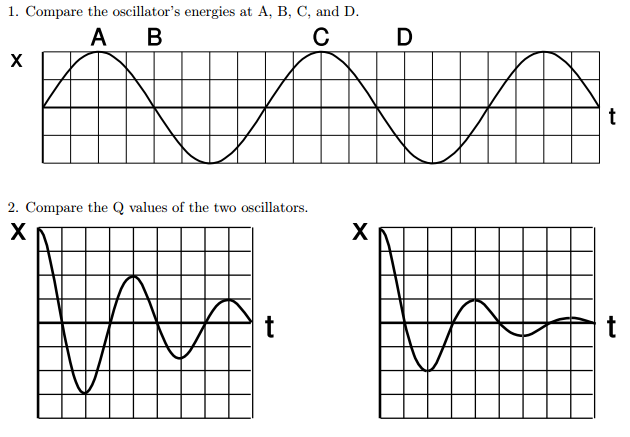
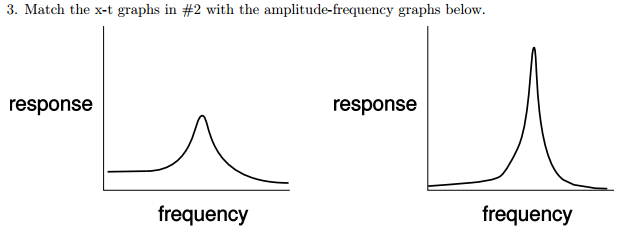
Exercise 18: Resonance
18.5 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.