18.4 Proofs  by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.

18.4 Proofs (optional)

Our first goal is to predict the amplitude of the steady-state vibrations as a function of the frequency of the driving force and the amplitude of the driving force. With that equation in hand, we will then prove statements 2, 3, and 4 from section 18.3. We assume without proof statement 1, that the steady-state motion occurs at the same frequency as the driving force.

As with the proof in chapter 17, we make use of the fact that a sinusoidal vibration is the same as the projection of circular motion onto a line. We visualize the system shown in figures k-m, in which the mass swings in a circle on the end of a spring. The spring does not actually change its length at all, but it appears to from the flattened perspective of a person viewing the system edge-on. The radius of the circle is the amplitude, `A`, of the vibrations as seen edge-on. The damping force can be imagined as a backward drag force supplied by some fluid through which the mass is moving. As usual, we assume that the damping is proportional to velocity, and we use the symbol `b` for the proportionality constant, `|F_d|=bv`. The driving force, represented by a hand towing the mass with a string, has a tangential component `|F_t|` which counteracts the damping force, `|F_t|=|F_d|`, and a radial component `F_r` which works either with or against the spring's force, depending on whether we are driving the system above or below its resonant frequency.

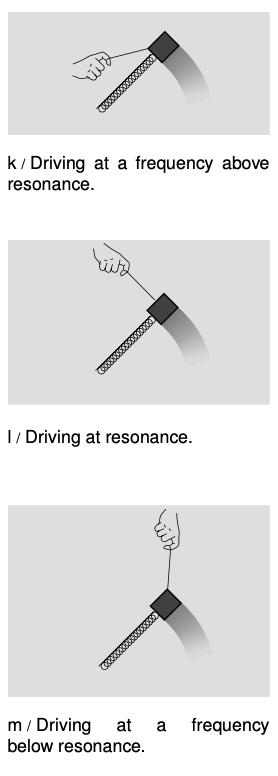The speed of the rotating mass is the circumference of the circle divided by the period, `v=2piA`/`T`, its acceleration (which is directly inward) is `a=v^2"/"r`, and Newton's second law gives `a=F"/"m`=`(kA+F_r)`/`m`. We write `f_o` for `1/(2pi)sqrt(k"/"m)`. Straightforward algebra yields

[1]  `F_r/F_t=(2pim)/(bf)(f^2-f_o^2)`.

This is the ratio of the wasted force to the useful force, and we see that it becomes zero when the system is driven at resonance.

The amplitude of the vibrations can be found by attacking the equation `|F_t|=bv=2pibAf`, which gives

[2]  `A=|Ft|/(2pibf)`. (2)

However, we wish to know the amplitude in terms of `|F|`, not `|F_t|`. From now on, let's drop the cumbersome magnitude symbols. With the Pythagorean theorem, it is easily proved that

[3]  `F_t=F/sqrt(1+(F_r/F_t)^2)`, (3)

and equations 1-3 can then be combined to give the final result

[4]  ` A = F/(2\pisqrt{4\pi^2m^2(f^2-f_{o}^2)^2+b^2f^2) `. 

 

Statement 2: maximum amplitude at resonance

Equation [4] makes it plausible that the amplitude is maximized when the system is driven at close to its resonant frequency. At `f=f_o`, the first term inside the square root vanishes, and this makes the denominator as small as possible, causing the amplitude to be as big as possible. (Actually this is only approximately true, because it is possible to make `A` a little bigger by decreasing `f`a little below `f_o`, which makes the second term smaller. This technical issue is addressed in homework problem 3 on page 477.)

Statement 3: amplitude at resonance proportional to `Q`

Equation [4] shows that the amplitude at resonance is proportional to `1`/`b`, and the `Q` of the system is inversely proportional to `b`, so the amplitude at resonance is proportional to `Q`.

Statement 4: FWHM related to `Q`

We will satisfy ourselves by proving only the proportionality `FWHMpropf_o`/`Q`, not the actual equation `FWHM=f_o`/`Q`. The energy is proportional to `A^2`, i.e., to the inverse of the quantity inside the square root in equation [4]. At resonance, the first term inside the square root vanishes, and the half-maximum points occur at frequencies for which the whole quantity inside the square root is double its value at resonance, i.e., when the two terms are equal. At the half-maximum points, we have

`f^2-f_o^2=(f_o±(FWHM)/2)^2-f_o^2`
`=±f_o*FWHM + 1/4FWHM^2`

If we assume that the width of the resonance is small compared to the resonant frequency, then the `FWHM^2` term is negligible compared to the `f_o*FWHM` term, and setting the terms in equation 4 equal to each other gives

`4pi^2m^2f_o(FWHM)^2=b^2f^2`.

We are assuming that the width of the resonance is small compared to the resonant frequency, so `f` and `f_o`can be taken as synonyms. Thus,

`FWHM=b/(2pim)`.

We wish to connect this to `Q`, which can be interpreted as the energy of the free (undriven) vibrations divided by the work done by damping in one cycle. The former equals `kA^2"/"2`, and the latter is proportional to the force, `bvpropbAf_o`, multiplied by the distance traveled, `A`. (This is only a proportionality, not an equation, since the force is not constant.) We therefore find that `Q` is proportional to `k"/"bf_o`. The equation for the `FWHM` can then be restated as a proportionality `FWHMpropk"/"Qf_ompropf_o`/`Q`.

18.4 Proofs  by Benjamin Crowell, Light and Matter  licensed under the Creative Commons Attribution-ShareAlike license.