The Bottle Coating Amount calculator computes the amount of coating material to cover the surface area of a bottle.
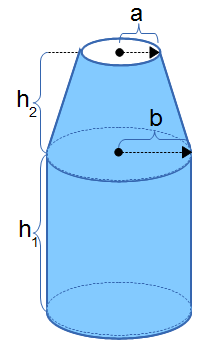
INSTRUCTIONS: Choose units and enter the following (see diagram):
- (a) Radius at Top Bottle
- (h2) Height of Tapered Neck
- (b) Base Radius
- (h1) Height of Base
- (t) Coating Thickness
- (n) Number of Bottles
Bottle Coating Volume (V): The calculator returns the volume of material in liters (milliliters). However, these can be automatically converted to many other area units (e.g. square inches or even acres) via the pull-down menu.
YouTube video instructions can be seen HERE. For the Volume of a Bottle, CLICK HERE. For the Mass of the Contents of a Bottle, CLICK HERE.
Bottle Calculators
- Surface Area of a Bottle: This computes the surface area of a bottle shaped object based on the dimensions.
- Mass of the Contents of a Bottle: This computes the weight or mass of a bottle shaped object based on the dimensions and the density of its contents.
- Volume of a Bottle: This computes the volume of a bottle shaped object based on the dimensions.
- Bottle Coating Amount: This computes the volume of material needed to coat the surface area of a bottle shaped object.
The Math
The formula used in this calculator is as follows:
`A = pi(a+b) sqrt(h_2^2+(b-a)^2) + 2*pi*b*h_1 + pi*b^2`
The surface area (A) includes several geometric shapes: the tapered neck, the cylindrical body and the circular bottom. You can see this in the three components of the formula:
- tapered neck (frustum of a cone): `A = pi(a+b)sqrt(h_2^2 + (b-a)^2)`
- cylindrical body (cylinder): `A = 2pi*b*h_1`
- circular bottom (circle): `A=pi*b^2`
NOTES
Geometrically, a bottle shaped object is the combination of right circular cone with a frustum defined by base radius (a) and top radius (b) and height (h2) in between and a cylinder of radius (b) and height (h1). The surface area is the sum of the surface of the cone frustum, the cylinder and the circle of the bottom. Note: this leave no surface area for the opening at the top.
