35.1 Electrons as waves by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
35.1 Electrons as waves
We started our journey into quantum physics by studying the random behavior of matter in radioactive decay, and then asked how randomness could be linked to the basic laws of nature governing light. The probability interpretation of wave-particle duality was strange and hard to accept, but it provided such a link. It is now natural to ask whether the same explanation could be applied to matter. If the fundamental building block of light, the photon, is a particle as well as a wave, is it possible that the basic units of matter, such as electrons, are waves as well as particles?
A young French aristocrat studying physics, Louis de Broglie (pronounced “broylee”), made exactly this suggestion in his 1923 Ph.D. thesis. His idea had seemed so far fetched that there was serious doubt about whether to grant him the degree. Einstein was asked for his opinion, and with his strong support, de Broglie got his degree.
Only two years later, American physicists C.J. Davisson and L. Germer confirmed de Broglie's idea by accident. They had been studying the scattering of electrons from the surface of a sample of nickel, made of many small crystals. (One can often see such a crystalline pattern on a brass doorknob that has been polished by repeated handling.) An accidental explosion occurred, and when they put their apparatus back together they observed something entirely different: the scattered electrons were now creating an interference pattern! This dramatic proof of the wave nature of matter came about because the nickel sample had been melted by the explosion and then resolidified as a single crystal. The nickel atoms, now nicely arranged in the regular rows and columns of a crystalline lattice, were acting as the lines of a diffraction grating. The new crystal was analogous to the type of ordinary diffraction grating in which the lines are etched on the surface of a mirror (a reflection grating) rather than the kind in which the light passes through the transparent gaps between the lines (a transmission grating).
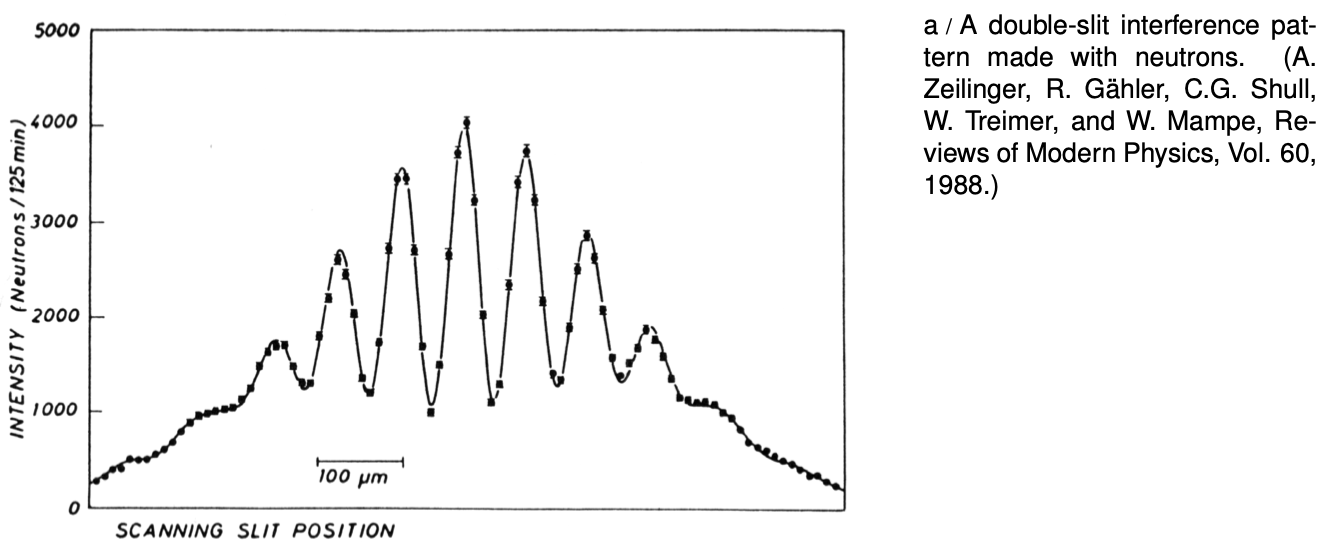
Although we will concentrate on the wave-particle duality of electrons because it is important in chemistry and the physics of atoms, all the other “particles” of matter you've learned about show wave properties as well. Figure a, for instance, shows a wave interference pattern of neutrons.
It might seem as though all our work was already done for us, and there would be nothing new to understand about electrons: they have the same kind of funny wave-particle duality as photons. That's almost true, but not quite. There are some important ways in which electrons differ significantly from photons:
- Electrons have mass, and photons don't.
- Photons always move at the speed of light, but electrons can move at any speed less than `c`.
- Photons don't have electric charge, but electrons do, so electric forces can act on them. The most important example is the atom, in which the electrons are held by the electric force of the nucleus.
- Electrons cannot be absorbed or emitted as photons are. Destroying an electron, or creating one out of nothing, would violate conservation of charge.
(In chapter 36 we will learn of one more fundamental way in which electrons differ from photons, for a total of five.)
Because electrons are different from photons, it is not immediately obvious which of the photon equations from chapter 34 can be applied to electrons as well. A particle property, the energy of one photon, is related to its wave properties via `E=hf` or, equivalently, `E=(hc)/lambda`. The momentum of a photon was given by `p=(hf)/c` or `p=h/lambda` (example 3 on page 948). Ultimately it was a matter of experiment to determine which of these equations, if any, would work for electrons, but we can make a quick and dirty guess simply by noting that some of the equations involve `c`, the speed of light, and some do not. Since `c` is irrelevant in the case of an electron, we might guess that the equations of general validity are those that do not have `c` in them:
This is essentially the reasoning that de Broglie went through, and experiments have confirmed these two equations for all the fundamental building blocks of light and matter, not just for photons and electrons.
The second equation, which I soft-pedaled in chapter 34, takes on a greater importance for electrons. This is first of all because the momentum of matter is more likely to be significant than the momentum of light under ordinary conditions, and also because force is the transfer of momentum, and electrons are affected by electrical forces.
Example 1: The wavelength of an elephant
`=>` What is the wavelength of a trotting elephant?
`=>` One may doubt whether the equation should be applied to an elephant, which is not just a single particle but a rather large collection of them. Throwing caution to the wind, however, we estimate the elephant's mass at `10^3` kg and its trotting speed at `10` m/s. Its wavelength is therefore roughly
`=h/(mv)`
`=(6.63×10^-34) J*s)/((10^3 kg)(10 m"/"s))`
`~10^(-37) ((kg*m^2"/"s^2)*s)/(kg*m"/"s)`
`=10^(-37) m.`
The wavelength found in this example is so fantastically small that we can be sure we will never observe any measurable wave phenomena with elephants. The result is numerically small because Planck's constant is so small, and as in some examples encountered previously, this smallness is in accord with the correspondence principle.
Although a smaller mass in the equation `lambda=h/(mv)` does result in a longer wavelength, the wavelength is still quite short even for individual electrons under typical conditions, as shown in the following example.
Example 2: The typical wavelength of an electron
`=>` Electrons in circuits and in atoms are typically moving through voltage differences on the order of `1 V`, so that a typical energy is `(e)(1 V)`, which is on the order of `10^(-19) J`. What is the wavelength of an electron with this amount of kinetic energy?
`=>` This energy is nonrelativistic, since it is much less than `mc^2`. Momentum and energy are therefore related by the nonrelativistic equation `KE=p^2/(2m)`. Solving for `p` and substituting in to the equation for the wavelength, we find
`=1.6×10^(-9) m`.
This is on the same order of magnitude as the size of an atom, which is no accident: as we will discuss in the next chapter in more detail, an electron in an atom can be interpreted as a standing wave. The smallness of the wavelength of a typical electron also helps to explain why the wave nature of electrons wasn't discovered until a hundred years after the wave nature of light. To scale the usual wave-optics devices such as diffraction gratings down to the size needed to work with electrons at ordinary energies, we need to make them so small that their parts are comparable in size to individual atoms. This is essentially what Davisson and Germer did with their nickel crystal.
self-check:
These remarks about the inconvenient smallness of electron wavelengths apply only under the assumption that the electrons have typical energies. What kind of energy would an electron have to have in order to have a longer wavelength that might be more convenient to work with?
(answer in the back of the PDF version of the book)
What kind of wave is it?
If a sound wave is a vibration of matter, and a photon is a vibration of electric and magnetic fields, what kind of a wave is an electron made of? The disconcerting answer is that there is no experimental “observable,” i.e., directly measurable quantity, to correspond to the electron wave itself. In other words, there are devices like microphones that detect the oscillations of air pressure in a sound wave, and devices such as radio receivers that measure the oscillation of the electric and magnetic fields in a light wave, but nobody has ever found any way to measure an electron wave directly.
We can of course detect the energy (or momentum) possessed by an electron just as we could detect the energy of a photon using a digital camera. (In fact I'd imagine that an unmodified digital camera chip placed in a vacuum chamber would detect electrons just as handily as photons.) But this only allows us to determine where the wave carries high probability and where it carries low probability. Probability is proportional to the square of the wave's amplitude, but measuring its square is not the same as measuring the wave itself. In particular, we get the same result by squaring either a positive number or its negative, so there is no way to determine the positive or negative sign of an electron wave.
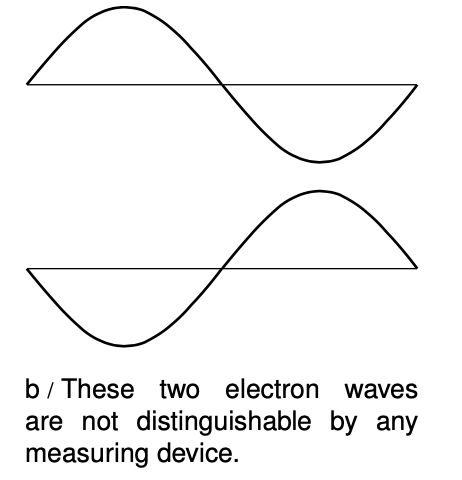 Most physicists tend toward the school of philosophy known as operationalism, which says that a concept is only meaningful if we can define some set of operations for observing, measuring, or testing it. According to a strict operationalist, then, the electron wave itself is a meaningless concept. Nevertheless, it turns out to be one of those concepts like love or humor that is impossible to measure and yet very useful to have around. We therefore give it a symbol, `Psi` (the capital Greek letter psi), and a special name, the electron wavefunction (because it is a function of the coordinates `x, y`, and `z` that specify where you are in space). It would be impossible, for example, to calculate the shape of the electron wave in a hydrogen atom without having some symbol for the wave. But when the calculation produces a result that can be compared directly to experiment, the final algebraic result will turn out to involve only `Psi^2`, which is what is observable, not `Psi` itself.
Most physicists tend toward the school of philosophy known as operationalism, which says that a concept is only meaningful if we can define some set of operations for observing, measuring, or testing it. According to a strict operationalist, then, the electron wave itself is a meaningless concept. Nevertheless, it turns out to be one of those concepts like love or humor that is impossible to measure and yet very useful to have around. We therefore give it a symbol, `Psi` (the capital Greek letter psi), and a special name, the electron wavefunction (because it is a function of the coordinates `x, y`, and `z` that specify where you are in space). It would be impossible, for example, to calculate the shape of the electron wave in a hydrogen atom without having some symbol for the wave. But when the calculation produces a result that can be compared directly to experiment, the final algebraic result will turn out to involve only `Psi^2`, which is what is observable, not `Psi` itself.
Since `Psi`, unlike `E` and `B`, is not directly measurable, we are free to make the probability equations have a simple form: instead of having the probability distribution equal to some funny constant multiplied by `Psi^2`, we simply define `Psi` so that the constant of proportionality is one:
`("probability distribution")=Psi^2`.
Since the probability distribution has units of `m^(-3)`, the units of `Psi` must be `m^(-3"/"2)`.
Discussion Question
A Frequency is oscillations per second, whereas wavelength is meters per oscillation. How could the equations `E=hf` and `p=h/lambda` be made to look more alike by using quantities that were more closely analogous? (This more symmetric treatment makes it easier to incorporate relativity into quantum mechanics, since relativity says that space and time are not entirely separate.)
35.1 Electrons as waves by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.