34.3 Wave-particle duality by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
34.3 Wave-particle duality

How can light be both a particle and a wave? We are now ready to resolve this seeming contradiction. Often in science when something seems paradoxical, it's because we either don't define our terms carefully, or don't test our ideas against any specific real-world situation. Let's define particles and waves as follows:
- Waves exhibit superposition, and specifically interference phenomena.
- Particles can only exist in whole numbers, not fractions.
As a real-world check on our philosophizing, there is one particular experiment that works perfectly. We set up a double-slit interference experiment that we know will produce a diffraction pattern if light is an honest-to-goodness wave, but we detect the light with a detector that is capable of sensing individual photons, e.g., a digital camera. To make it possible to pick out individual dots from individual photons, we must use filters to cut down the intensity of the light to a very low level, just as in the photos by Prof. Page in section 34.1. The whole thing is sealed inside a light-tight box. The results are shown in figure i. (In fact, the similar figures in section 34.1 are simply cutouts from these figures.)
 Neither the pure wave theory nor the pure particle theory can explain the results. If light was only a particle and not a wave, there would be no interference effect. The result of the experiment would be like firing a hail of bullets through a double slit, j. Only two spots directly behind the slits would be hit.
Neither the pure wave theory nor the pure particle theory can explain the results. If light was only a particle and not a wave, there would be no interference effect. The result of the experiment would be like firing a hail of bullets through a double slit, j. Only two spots directly behind the slits would be hit.
If, on the other hand, light was only a wave and not a particle, we would get the same kind of diffraction pattern that would happen with a water wave, k. There would be no discrete dots in the photo, only a diffraction pattern that shaded smoothly between light and dark.
Applying the definitions to this experiment, light must be both a particle and a wave. It is a wave because it exhibits interference effects. At the same time, the fact that the photographs contain discrete dots is a direct demonstration that light refuses to be split into units of less than a single photon. There can only be whole numbers of photons: four photons in figure i/3, for example.
A wrong interpretation: photons interfering with each other
One possible interpretation of wave-particle duality that occurred to physicists early in the game was that perhaps the interference effects came from photons interacting with each other. By analogy, a water wave consists of moving water molecules, and interference of water waves results ultimately from all the mutual pushes and pulls of the molecules. This interpretation was conclusively disproved by G.I. Taylor, a student at Cambridge. The demonstration by Prof. Page that we've just been discussing is essentially a modernized version of Taylor's work. Taylor reasoned that if interference effects came from photons interacting with each other, a bare minimum of two photons would have to be present at the same time to produce interference. By making the light source extremely dim, we can be virtually certain that there are never two photons in the box at the same time. In figure i, the intensity of the light has been cut down so much by the absorbers that if it was in the open, the average separation between photons would be on the order of a kilometer! At any given moment, the number of photons in the box is most likely to be zero. It is virtually certain that there were never two photons in the box at once.
The concept of a photon's path is undefined.
 If a single photon can demonstrate double-slit interference, then which slit did it pass through? The unavoidable answer must be that it passes through both! This might not seem so strange if we think of the photon as a wave, but it is highly counterintuitive if we try to visualize it as a particle. The moral is that we should not think in terms of the path of a photon. Like the fully human and fully divine Jesus of Christian theology, a photon is supposed to be 100% wave and 100% particle. If a photon had a well defined path, then it would not demonstrate wave superposition and interference effects, contradicting its wave nature. (In the next chapter we will discuss the Heisenberg uncertainty principle, which gives a numerical way of approaching this issue.)
If a single photon can demonstrate double-slit interference, then which slit did it pass through? The unavoidable answer must be that it passes through both! This might not seem so strange if we think of the photon as a wave, but it is highly counterintuitive if we try to visualize it as a particle. The moral is that we should not think in terms of the path of a photon. Like the fully human and fully divine Jesus of Christian theology, a photon is supposed to be 100% wave and 100% particle. If a photon had a well defined path, then it would not demonstrate wave superposition and interference effects, contradicting its wave nature. (In the next chapter we will discuss the Heisenberg uncertainty principle, which gives a numerical way of approaching this issue.)
Another wrong interpretation: the pilot wave hypothesis
A second possible explanation of wave-particle duality was taken seriously in the early history of quantum mechanics. What if the photon particle is like a surfer riding on top of its accompanying wave? As the wave travels along, the particle is pushed, or “piloted” by it. Imagining the particle and the wave as two separate entities allows us to avoid the seemingly paradoxical idea that a photon is both at once. The wave happily does its wave tricks, like superposition and interference, and the particle acts like a respectable particle, resolutely refusing to be in two different places at once. If the wave, for instance, undergoes destructive interference, becoming nearly zero in a particular region of space, then the particle simply is not guided into that region.
The problem with the pilot wave interpretation is that the only way it can be experimentally tested or verified is if someone manages to detach the particle from the wave, and show that there really are two entities involved, not just one. Part of the scientific method is that hypotheses are supposed to be experimentally testable. Since nobody has ever managed to separate the wavelike part of a photon from the particle part, the interpretation is not useful or meaningful in a scientific sense.
The probability interpretation
The correct interpretation of wave-particle duality is suggested by the random nature of the experiment we've been discussing: even though every photon wave/particle is prepared and released in the same way, the location at which it is eventually detected by the digital camera is different every time. The idea of the probability interpretation of wave-particle duality is that the location of the photon-particle is random, but the probability that it is in a certain location is higher where the photon-wave's amplitude is greater.
More specifically, the probability distribution of the particle must be proportional to the square of the wave's amplitude,
`("probability distribution")propto("amplitude")^2`.
This follows from the correspondence principle and from the fact that a wave's energy density is proportional to the square of its amplitude. If we run the double-slit experiment for a long enough time, the pattern of dots fills in and becomes very smooth as would have been expected in classical physics. To preserve the correspondence between classical and quantum physics, the amount of energy deposited in a given region of the picture over the long run must be proportional to the square of the wave's amplitude. The amount of energy deposited in a certain area depends on the number of photons picked up, which is proportional to the probability of finding any given photon there.
Example 4: A microwave oven
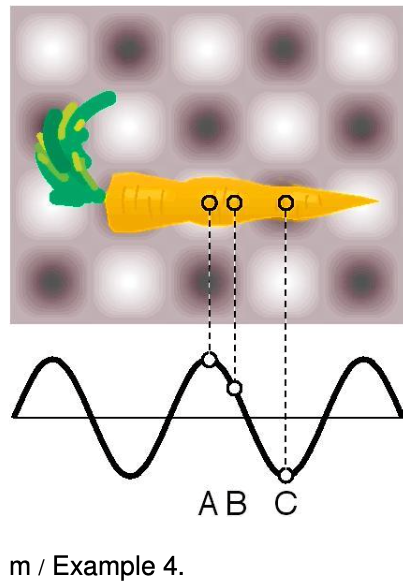 `=>` The figure shows two-dimensional (top) and one-dimensional (bottom) representations of the standing wave inside a microwave oven. Gray represents zero field, and white and black signify the strongest fields, with white being a field that is in the opposite direction compared to black. Compare the probabilities of detecting a microwave photon at points `A`, `B`, and `C`.
`=>` The figure shows two-dimensional (top) and one-dimensional (bottom) representations of the standing wave inside a microwave oven. Gray represents zero field, and white and black signify the strongest fields, with white being a field that is in the opposite direction compared to black. Compare the probabilities of detecting a microwave photon at points `A`, `B`, and `C`.
`=>` `A` and `C` are both extremes of the wave, so the probabilities of detecting a photon at `A` and `C` are equal. It doesn't matter that we have represented `C` as negative and `A` as positive, because it is the square of the amplitude that is relevant. The amplitude at `B` is about `1`/`2` as much as the others, so the probability of detecting a photon there is about `1`/`4` as much.
The probability interpretation was disturbing to physicists who had spent their previous careers working in the deterministic world of classical physics, and ironically the most strenuous objections against it were raised by Einstein, who had invented the photon concept in the first place. The probability interpretation has nevertheless passed every experimental test, and is now as well established as any part of physics.
An aspect of the probability interpretation that has made many people uneasy is that the process of detecting and recording the photon's position seems to have a magical ability to get rid of the wavelike side of the photon's personality and force it to decide for once and for all where it really wants to be. But detection or measurement is after all only a physical process like any other, governed by the same laws of physics. We will postpone a detailed discussion of this issue until the following chapter, since a measuring device like a digital camera is made of matter, but we have so far only discussed how quantum mechanics relates to light.
Example 5: What is the proportionality constant?
`=>` What is the proportionality constant that would make an actual equation out of `("probability distribution")propto("amplitude")^2`?
`=>` The probability that the photon is in a certain small region of volume `v` should equal the fraction of the wave's energy that is within that volume. For a sinusoidal wave, which has a single, well-defined frequency `f`, this gives
`P=("energy in volume "v)/"energy of photon"`
`=("energy in volume "v)/(hf)`.
We assume `v` is small enough so that the electric and magnetic fields are nearly constant throughout it. We then have
`P = ((1/(8pik)|E|^2 + c^2/(8pik)|B|^2)v)/(hf)`.
We can simplify this formidable looking expression by recognizing that in a plane wave, `|E|` and `|B|` are related by `|E|=c|B|`. This implies (problem 20, p. 705), that the electric and magnetic fields each contribute half the total energy, so we can simplify the result to
`P=2((1/(8pik)|E|^2)v)/(hf)`
`=(v/(4pikhf)|E|^2)`.
The probability is proportional to the square of the wave's amplitude, as advertised.3
Discussion Questions
A In example 4 on page 952, about the carrot in the microwave oven, show that it would be nonsensical to have probability be proportional to the field itself, rather than the square of the field.
B Einstein did not try to reconcile the wave and particle theories of light, and did not say much about their apparent inconsistency. Einstein basically visualized a beam of light as a stream of bullets coming from a machine gun. In the photoelectric effect, a photon “bullet” would only hit one atom, just as a real bullet would only hit one person. Suppose someone reading his 1905 paper wanted to interpret it by saying that Einstein's so-called particles of light are simply short wave-trains that only occupy a small region of space. Comparing the wavelength of visible light (a few hundred nm) to the size of an atom (on the order of 0.1 nm), explain why this poses a difficulty for reconciling the particle and wave theories.
C Can a white photon exist?
D In double-slit diffraction of photons, would you get the same pattern of dots on the digital camera image if you covered one slit? Why should it matter whether you give the photon two choices or only one?
34.3 Wave-particle duality by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.