31.7 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
refraction — the change in direction that occurs when a wave encounters the interface between two media
index of refraction — an optical property of matter; the speed of light in a vacuum divided by the speed of light in the substance in question
Notation
`n` — the index of refraction
Summary
Refraction is a change in direction that occurs when a wave encounters the interface between two media. Together, refraction and reflection account for the basic principles behind nearly all optical devices.
Snell discovered the equation for refraction,
`n_1sintheta_1=n_2sintheta_2`,
[angles measured with respect to the normal] through experiments with light rays, long before light was proven to be a wave. Snell's law can be proven based on the geometrical behavior of waves. Here `n` is the index of refraction. Snell invented this quantity to describe the refractive properties of various substances, but it was later found to be related to the speed of light in the substance,
[Private Equation],
where `c` is the speed of light in a vacuum. In general a material's index of refraction is different for different wavelengths of light.
As discussed in chapter 20, any wave is partially transmitted and partially reflected at the boundary between two media in which its speeds are different. It is not particularly important to know the equation that tells what fraction is transmitted (and thus refracted), but important technologies such as fiber optics are based on the fact that this fraction becomes zero for sufficiently oblique angles. This phenomenon is referred to as total internal reflection. It occurs when there is no angle that satisfies Snell's law.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
1. Suppose a converging lens is constructed of a type of plastic whose index of refraction is less than that of water. How will the lens's behavior be different if it is placed underwater?
2. There are two main types of telescopes, refracting (using a lens) and reflecting (using a mirror, as in figure i on p. 838). (Some telescopes use a mixture of the two types of elements: the light first encounters a large curved mirror, and then goes through an eyepiece that is a lens. To keep things simple, assume no eyepiece is used.) What implications would the color-dependence of focal length have for the relative merits of the two types of telescopes? Describe the case where an image is formed of a white star. You may find it helpful to draw a ray diagram.
3. Based on Snell's law, explain why rays of light passing through the edges of a converging lens are bent more than rays passing through parts closer to the center. It might seem like it should be the other way around, since the rays at the edge pass through less glass --- shouldn't they be affected less? In your answer:
- Include a ray diagram showing a huge, full-page, close-up view of the relevant part of the lens.
- Make use of the fact that the front and back surfaces aren't always parallel; a lens in which the front and back surfaces are always parallel doesn't focus light at all, so if your explanation doesn't make use of this fact, your argument must be incorrect.
- Make sure your argument still works even if the rays don't come in parallel to the axis.
4. When you take pictures with a camera, the distance between the lens and the film has to be adjusted, depending on the distance at which you want to focus. This is done by moving the lens. If you want to change your focus so that you can take a picture of something farther away, which way do you have to move the lens? Explain using ray diagrams. [Based on a problem by Eric Mazur.]
5. (a) Light is being reflected diffusely from an object 1.000 m underwater. The light that comes up to the surface is refracted at the water-air interface. If the refracted rays all appear to come from the same point, then there will be a virtual image of the object in the water, above the object's actual position, which will be visible to an observer above the water. Consider three rays, A, B and C, whose angles in the water with respect to the normal are `theta_i=0.000°`, `1.000°` and `20.000°` respectively. Find the depth of the point at which the refracted parts of A and B appear to have intersected, and do the same for A and C. Show that the intersections are at nearly the same depth, but not quite. [Check: The difference in depth should be about 4 cm.]
(b) Since all the refracted rays do not quite appear to have come from the same point, this is technically not a virtual image. In practical terms, what effect would this have on what you see?
(c) In the case where the angles are all small, use algebra and trig to show that the refracted rays do appear to come from the same point, and find an equation for the depth of the virtual image. Do not put in any numerical values for the angles or for the indices of refraction --- just keep them as symbols. You will need the approximation `sinapproxthetaapproxtanthetaapproxtheta`, which is valid for small angles measured in radians. `***`
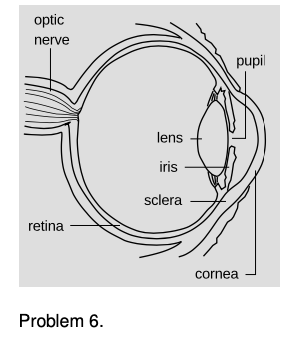 6. The drawing shows the anatomy of the human eye, at twice life size. Find the radius of curvature of the outer surface of the cornea by measurements on the figure, and then derive the focal length of the air-cornea interface, where almost all the focusing of light occurs. You will need to use physical reasoning to modify the lensmaker's equation for the case where there is only a single refracting surface. Assume that the index of refraction of the cornea is essentially that of water. `***`
6. The drawing shows the anatomy of the human eye, at twice life size. Find the radius of curvature of the outer surface of the cornea by measurements on the figure, and then derive the focal length of the air-cornea interface, where almost all the focusing of light occurs. You will need to use physical reasoning to modify the lensmaker's equation for the case where there is only a single refracting surface. Assume that the index of refraction of the cornea is essentially that of water. `***`
7. When swimming underwater, why is your vision made much clearer by wearing goggles with flat pieces of glass that trap air behind them? [Hint: You can simplify your reasoning by considering the special case where you are looking at an object far away, and along the optic axis of the eye.]
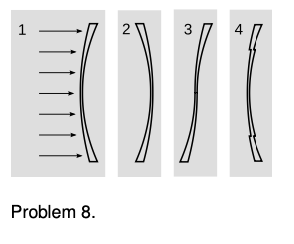 8. The figure shows four lenses. Lens 1 has two spherical surfaces. Lens 2 is the same as lens 1 but turned around. Lens 3 is made by cutting through lens 1 and turning the bottom around. Lens 4 is made by cutting a central circle out of lens 1 and recessing it.
8. The figure shows four lenses. Lens 1 has two spherical surfaces. Lens 2 is the same as lens 1 but turned around. Lens 3 is made by cutting through lens 1 and turning the bottom around. Lens 4 is made by cutting a central circle out of lens 1 and recessing it.
(a) A parallel beam of light enters lens 1 from the left, parallel to its axis. Reasoning based on Snell's law, will the beam emerging from the lens be bent inward, or outward, or will it remain parallel to the axis? Explain your reasoning. As part of your answer, make a huge drawing of one small part of the lens, and apply Snell's law at both interfaces. Recall that rays are bent more if they come to the interface at a larger angle with respect to the normal.
(b) What will happen with lenses 2, 3, and 4? Explain. Drawings are not necessary.
9. Prove that the principle of least time leads to Snell's law. `***`
10. An object is more than one focal length from a converging lens. (a) Draw a ray diagram. (b) Using reasoning like that developed in chapter 30, determine the positive and negative signs in the equation `1"/"f=±1"/"d_i±1"/"d_o`. (c) The images of the rose in section 4.2 were made using a lens with a focal length of 23 cm. If the lens is placed 80 cm from the rose, locate the image. `sqrt`
11. An object is less than one focal length from a converging lens. (a) Draw a ray diagram. (b) Using reasoning like that developed in chapter 30, determine the positive and negative signs in the equation `1"/"f=+-1"/"d_i+-1"/"d_o`. (c) The images of the rose in section 4.2 were made using a lens with a focal length of 23 cm. If the lens is placed 10 cm from the rose, locate the image. `sqrt`
12. Nearsighted people wear glasses whose lenses are diverging. (a) Draw a ray diagram. For simplicity pretend that there is no eye behind the glasses. (b) Using reasoning like that developed in chapter 30, determine the positive and negative signs in the equation `1"/"f=+-1"/"d_i+-1"/"d_o`. (c) If the focal length of the lens is 50.0 cm, and the person is looking at an object at a distance of 80.0 cm, locate the image. `sqrt`
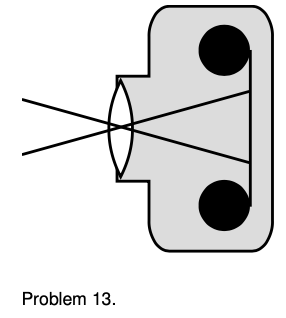 13. Two standard focal lengths for camera lenses are 50 mm (standard) and 28 mm (wide-angle). To see how the focal lengths relate to the angular size of the field of view, it is helpful to visualize things as represented in the figure. Instead of showing many rays coming from the same point on the same object, as we normally do, the figure shows two rays from two different objects. Although the lens will intercept infinitely many rays from each of these points, we have shown only the ones that pass through the center of the lens, so that they suffer no angular deflection. (Any angular deflection at the front surface of the lens is canceled by an opposite deflection at the back, since the front and back surfaces are parallel at the lens's center.) What is special about these two rays is that they are aimed at the edges of one 35-mm-wide frame of film; that is, they show the limits of the field of view. Throughout this problem, we assume that `d_o` is much greater than `d_i`. (a) Compute the angular width of the camera's field of view when these two lenses are used. (b) Use small-angle approximations to find a simplified equation for the angular width of the field of view, `theta`, in terms of the focal length, `f`, and the width of the film, `w`. Your equation should not have any trig functions in it. Compare the results of this approximation with your answers from part a. (c) Suppose that we are holding constant the aperture (amount of surface area of the lens being used to collect light). When switching from a 50-mm lens to a 28-mm lens, how many times longer or shorter must the exposure be in order to make a properly developed picture, i.e., one that is not under- or overexposed? [Based on a problem by Arnold Arons.]
13. Two standard focal lengths for camera lenses are 50 mm (standard) and 28 mm (wide-angle). To see how the focal lengths relate to the angular size of the field of view, it is helpful to visualize things as represented in the figure. Instead of showing many rays coming from the same point on the same object, as we normally do, the figure shows two rays from two different objects. Although the lens will intercept infinitely many rays from each of these points, we have shown only the ones that pass through the center of the lens, so that they suffer no angular deflection. (Any angular deflection at the front surface of the lens is canceled by an opposite deflection at the back, since the front and back surfaces are parallel at the lens's center.) What is special about these two rays is that they are aimed at the edges of one 35-mm-wide frame of film; that is, they show the limits of the field of view. Throughout this problem, we assume that `d_o` is much greater than `d_i`. (a) Compute the angular width of the camera's field of view when these two lenses are used. (b) Use small-angle approximations to find a simplified equation for the angular width of the field of view, `theta`, in terms of the focal length, `f`, and the width of the film, `w`. Your equation should not have any trig functions in it. Compare the results of this approximation with your answers from part a. (c) Suppose that we are holding constant the aperture (amount of surface area of the lens being used to collect light). When switching from a 50-mm lens to a 28-mm lens, how many times longer or shorter must the exposure be in order to make a properly developed picture, i.e., one that is not under- or overexposed? [Based on a problem by Arnold Arons.]
14. A nearsighted person is one whose eyes focus light too strongly, and who is therefore unable to relax the lens inside her eye sufficiently to form an image on her retina of an object that is too far away.
(a) Draw a ray diagram showing what happens when the person tries, with uncorrected vision, to focus at infinity.
(b) What type of lenses do her glasses have? Explain.
(c) Draw a ray diagram showing what happens when she wears glasses. Locate both the image formed by the glasses and the final image.
(d) Suppose she sometimes uses contact lenses instead of her glasses. Does the focal length of her contacts have to be less than, equal to, or greater than that of her glasses? Explain.
15. Diamond has an index of refraction of 2.42, and part of the reason diamonds sparkle is that this encourages a light ray to undergo many total internal reflections before it emerges. (a) Calculate the critical angle at which total internal reflection occurs in diamond. (answer check available at lightandmatter.com) (b) Explain the interpretation of your result: Is it measured from the normal, or from the surface? Is it a minimum angle for total internal reflection, or is it a maximum? How would the critical angle have been different for a substance such as glass or plastic, with a lower index of refraction? `sqrt`
16. Fred's eyes are able to focus on things as close as 5.0 cm. Fred holds a magnifying glass with a focal length of 3.0 cm at a height of 2.0 cm above a flatworm. (a) Locate the image, and find the magnification. (b) Without the magnifying glass, from what distance would Fred want to view the flatworm to see its details as well as possible? With the magnifying glass? (c) Compute the angular magnification.
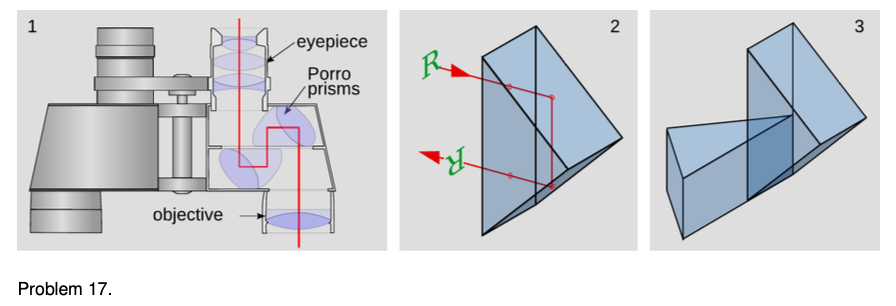
17. Panel 1 of the figure shows the optics inside a pair of binoculars. They are essentially a pair of telescopes, one for each eye. But to make them more compact, and allow the eyepieces to be the right distance apart for a human face, they incorporate a set of eight prisms, which fold the light path. In addition, the prisms make the image upright. Panel 2 shows one of these prisms, known as a Porro prism. The light enters along a normal, undergoes two total internal reflections at angles of 45 degrees with respect to the back surfaces, and exits along a normal. The image of the letter R has been flipped across the horizontal. Panel 3 shows a pair of these prisms glued together. The image will be flipped across both the horizontal and the vertical, which makes it oriented the right way for the user of the binoculars.
(a) Find the minimum possible index of refraction for the glass used in the prisms.
(b) For a material of this minimal index of refraction, find the fraction of the incoming light that will be lost to reflection in the four Porro prisms on a each side of a pair of binoculars. (See ch. 20.) In real, high-quality binoculars, the optical surfaces of the prisms have antireflective coatings, but carry out your calculation for the case where there is no such coating.
(c) Discuss the reasons why a designer of binoculars might or might not want to use a material with exactly the index of refraction found in part a. `***`
18. It would be annoying if your eyeglasses produced a magnified or reduced image. Prove that when the eye is very close to a lens, and the lens produces a virtual image, the angular magnification is always approximately equal to 1 (regardless of whether the lens is diverging or converging).
19. A typical mirror consists of a pane of glass of thickness `t` and index of refraction `n`, “silvered” on the back with a reflective coating. Let `d_o` and `d_i` be measured from the back of the mirror. Show that `d_i=d_o-2(1-1"/"n)t`. Use the result of, and make the approximation employed in, problem 5c. As a check on your result, consider separately the special values of `n` and `t` that would recover the case without any glass.
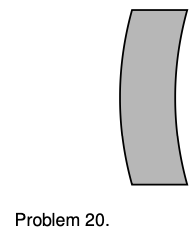 20. The figure shows a lens with surfaces that are curved, but whose thickness is constant along any horizontal line. Use the lensmaker's equation to prove that this “lens” is not really a lens at all.(solution in the pdf version of the book)
20. The figure shows a lens with surfaces that are curved, but whose thickness is constant along any horizontal line. Use the lensmaker's equation to prove that this “lens” is not really a lens at all.(solution in the pdf version of the book)
21. Estimate the radii of curvature of the two optical surfaces in the eye of the jumping spider in figure s on p. 878. Use physical reasoning to modify the lensmaker's equation for a case like this one, in which there are three indices of refraction `n_1` (air), `n_2` (lens), and `n_3` (the material behind the lens), and `n_1!=n_3`. Show that the interface between `n_2` and `n_3` contributes negligibly to focusing, and verify that the image is produced at approximately the right place in the eye when the object is far away. As a check on your result, direct optical measurements by M.F. Land in 1969 gave `f=512 mum`. `sqrt`
How strong are your glasses?
This exercise was created by Dan MacIsaac.
Equipment:
- eyeglasses
- diverging lenses for students who don't wear glasses, or who use converging glasses
- rulers and metersticks
- scratch paper
- marking pens
Most people who wear glasses have glasses whose lenses are diverging, which allows them to focus on objects far away. Such a lens cannot form a real image, so its focal length cannot be measured as easily as that of an converging lens. In this exercise you will determine the focal length of your own glasses by taking them off, holding them at a distance from your face, and looking through them at a set of parallel lines on a piece of paper. The lines will be reduced (the lens's magnification is less than one), and by adjusting the distance between the lens and the paper, you can make the magnification equal 1/2 exactly, so that two spaces between lines as seen through the lens fit into one space as seen simultaneously to the side of the lens. This object distance can be used in order to find the focal length of the lens.
1. Does this technique really measure magnification or does it measure angular magnification? What can you do in your experiment in order to make these two quantities nearly the same, so the math is simpler?
2. Before taking any numerical data, use algebra to find the focal length of the lens in terms of `d_o`, the object distance that results in a magnification of 1/2.
3. Use a marker to draw three evenly spaced parallel lines on the paper. (A spacing of a few cm works well.) Measure the object distance that results in a magnification of 1/2, and determine the focal length of your lens.
31.7 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.