25.3 Voltage and current by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
25.3 Voltage and current
What is physically happening in one of these oscillating circuits? Let's first look at the mechanical case, and then draw the analogy to the circuit. For simplicity, let's ignore the existence of damping, so there is no friction in the mechanical oscillator, and no resistance in the electrical one.
Suppose we take the mechanical oscillator and pull the mass away from equilibrium, then release it. Since friction tends to resist the spring's force, we might naively expect that having zero friction would allow the mass to leap instantaneously to the equilibrium position. This can't happen, however, because the mass would have to have infinite velocity in order to make such an instantaneous leap. Infinite velocity would require infinite kinetic energy, but the only kind of energy that is available for conversion to kinetic is the energy stored in the spring, and that is finite, not infinite. At each step on its way back to equilibrium, the mass's velocity is controlled exactly by the amount of the spring's energy that has so far been converted into kinetic energy. After the mass reaches equilibrium, it overshoots due to its own momentum. It performs identical oscillations on both sides of equilibrium, and it never loses amplitude because friction is not available to convert mechanical energy into heat.
Now with the electrical oscillator, the analog of position is charge. Pulling the mass away from equilibrium is like depositing charges `+q` and `-q` on the plates of the capacitor. Since resistance tends to resist the flow of charge, we might imagine that with no friction present, the charge would instantly flow through the inductor (which is, after all, just a piece of wire), and the capacitor would discharge instantly. However, such an instant discharge is impossible, because it would require infinite current for one instant. Infinite current would create infinite magnetic fields surrounding the inductor, and these fields would have infinite energy. Instead, the rate of flow of current is controlled at each instant by the relationship between the amount of energy stored in the magnetic field and the amount of current that must exist in order to have that strong a field. After the capacitor reaches `q=0`, it overshoots. The circuit has its own kind of electrical “inertia,” because if charge was to stop flowing, there would have to be zero current through the inductor. But the current in the inductor must be related to the amount of energy stored in its magnetic fields. When the capacitor is at `q=0`, all the circuit's energy is in the inductor, so it must therefore have strong magnetic fields surrounding it and quite a bit of current going through it.
The only thing that might seem spooky here is that we used to speak as if the current in the inductor caused the magnetic field, but now it sounds as if the field causes the current. Actually this is symptomatic of the elusive nature of cause and effect in physics. It's equally valid to think of the cause and effect relationship in either way. This may seem unsatisfying, however, and for example does not really get at the question of what brings about a voltage difference across the resistor (in the case where the resistance is finite); there must be such a voltage difference, because without one, Ohm's law would predict zero current through the resistor.
Voltage, then, is what is really missing from our story so far.
Let's start by studying the voltage across a capacitor. Voltage is electrical potential energy per unit charge, so the voltage difference between the two plates of the capacitor is related to the amount by which its energy would increase if we increased the absolute values of the charges on the plates from `q` to `q+Deltaq`:
`V_C=(E_q+Delta_q-E_q)"/"Deltaq`
`=(DeltaE_C)/(Deltaq)`
`=Delta/(Deltaq)(1/(2C)q^2)`
`=q/C`
 Many books use this as the definition of capacitance. This equation, by the way, probably explains the historical reason why `C` was defined so that the energy was inversely proportional to `C` for a given value of `C`: the people who invented the definition were thinking of a capacitor as a device for storing charge rather than energy, and the amount of charge stored for a fixed voltage (the charge “capacity”) is proportional to `C`.
Many books use this as the definition of capacitance. This equation, by the way, probably explains the historical reason why `C` was defined so that the energy was inversely proportional to `C` for a given value of `C`: the people who invented the definition were thinking of a capacitor as a device for storing charge rather than energy, and the amount of charge stored for a fixed voltage (the charge “capacity”) is proportional to `C`.
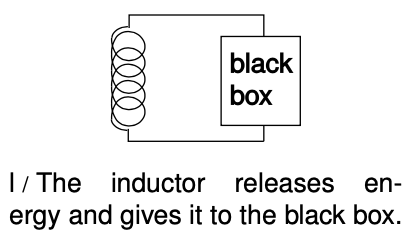
In the case of an inductor, we know that if there is a steady, constant current flowing through it, then the magnetic field is constant, and so is the amount of energy stored; no energy is being exchanged between the inductor and any other circuit element. But what if the current is changing? The magnetic field is proportional to the current, so a change in one implies a change in the other. For concreteness, let's imagine that the magnetic field and the current are both decreasing. The energy stored in the magnetic field is therefore decreasing, and by conservation of energy, this energy can't just go away --- some other circuit element must be taking energy from the inductor. The simplest example, shown in figure l, is a series circuit consisting of the inductor plus one other circuit element. It doesn't matter what this other circuit element is, so we just call it a black box, but if you like, we can think of it as a resistor, in which case the energy lost by the inductor is being turned into heat by the resistor. The junction rule tells us that both circuit elements have the same current through them, so `I` could refer to either one, and likewise the loop rule tells us `V_"inductor"+V_"black box"=0`, so the two voltage drops have the same absolute value, which we can refer to as `V`. Whatever the black box is, the rate at which it is taking energy from the inductor is given by `|P|=|I⋅V|`, so
`|IV|=|(DeltaE_L)/(Deltat)|`
`=|Delta/(Deltat)(1/(2)LI^2)|`
`=|LI (DeltaI)/(Deltat)|`,
or
which in many books is taken to be the definition of inductance. The direction of the voltage drop (plus or minus sign) is such that the inductor resists the change in current.
There's one very intriguing thing about this result. Suppose, for concreteness, that the black box in figure l is a resistor, and that the inductor's energy is decreasing, and being converted into heat in the resistor. The voltage drop across the resistor indicates that it has an electric field across it, which is driving the current. But where is this electric field coming from? There are no charges anywhere that could be creating it! What we've discovered is one special case of a more general principle, the principle of induction: a changing magnetic field creates an electric field, which is in addition to any electric field created by charges. (The reverse is also true: any electric field that changes over time creates a magnetic field.) Induction forms the basis for such technologies as the generator and the transformer, and ultimately it leads to the existence of light, which is a wave pattern in the electric and magnetic fields. These are all topics for chapter 24, but it's truly remarkable that we could come to this conclusion without yet having learned any details about magnetism.
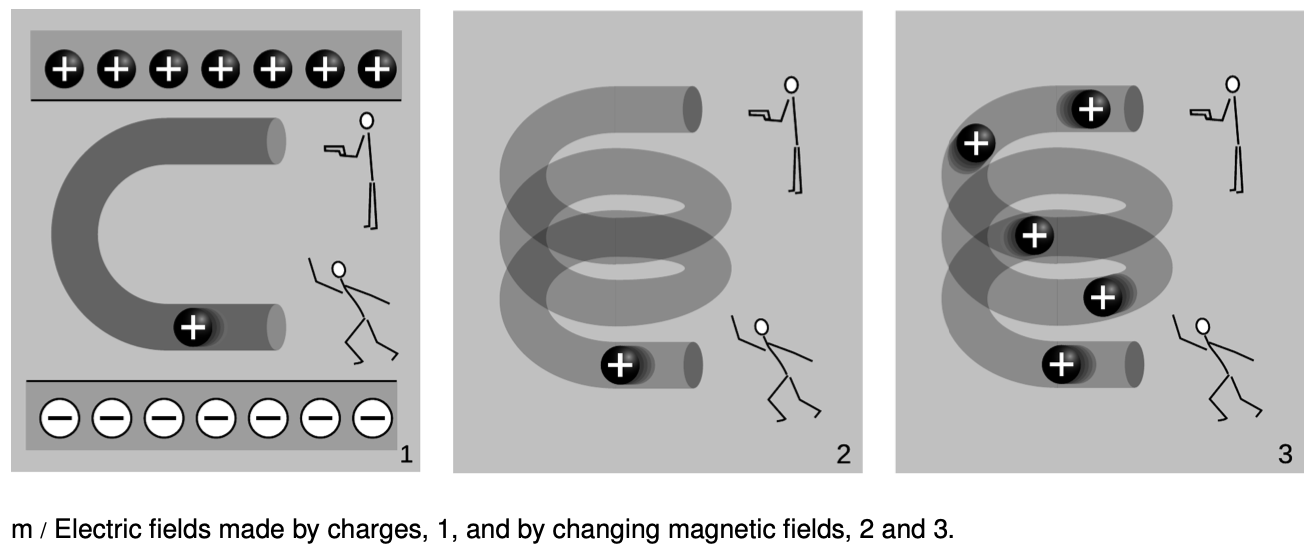
The cartoons in figure m compares electric fields made by charges, 1, to electric fields made by changing magnetic fields, 2-3. In m/1, two physicists are in a room whose ceiling is positively charged and whose floor is negatively charged. The physicist on the bottom throws a positively charged bowling ball into the curved pipe. The physicist at the top uses a radar gun to measure the speed of the ball as it comes out of the pipe. They find that the ball has slowed down by the time it gets to the top. By measuring the change in the ball's kinetic energy, the two physicists are acting just like a voltmeter. They conclude that the top of the tube is at a higher voltage than the bottom of the pipe. A difference in voltage indicates an electric field, and this field is clearly being caused by the charges in the floor and ceiling.
In m/2, there are no charges anywhere in the room except for the charged bowling ball. Moving charges make magnetic fields, so there is a magnetic field surrounding the helical pipe while the ball is moving through it. A magnetic field has been created where there was none before, and that field has energy. Where could the energy have come from? It can only have come from the ball itself, so the ball must be losing kinetic energy. The two physicists working together are again acting as a voltmeter, and again they conclude that there is a voltage difference between the top and bottom of the pipe. This indicates an electric field, but this electric field can't have been created by any charges, because there aren't any in the room. This electric field was created by the change in the magnetic field.
The bottom physicist keeps on throwing balls into the pipe, until the pipe is full of balls, m/3, and finally a steady current is established. While the pipe was filling up with balls, the energy in the magnetic field was steadily increasing, and that energy was being stolen from the balls' kinetic energy. But once a steady current is established, the energy in the magnetic field is no longer changing. The balls no longer have to give up energy in order to build up the field, and the physicist at the top finds that the balls are exiting the pipe at full speed again. There is no voltage difference any more. Although there is a current, `DeltaI"/"Deltat` is zero.
Discussion Question
A What happens when the physicist at the bottom in figure m/3 starts getting tired, and decreases the current?
25.3 Voltage and current by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.