22.9 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
Summary
Vocabulary
field — a property of a point in space describing the forces that would be exerted on a particle if it was there
sink — a point at which field vectors converge
source — a point from which field vectors diverge; often used more inclusively to refer to points of either convergence or divergence
electric field — the force per unit charge exerted on a test charge at a given point in space
gravitational field — the force per unit mass exerted on a test mass at a given point in space
electric dipole — an object that has an imbalance between positive charge on one side and negative charge on the other; an object that will experience a torque in an electric field
Notation
`g`— the gravitational field
`E`— the electric field
`D` — an electric dipole moment
Other Notation
`d`, `p`, `m` — other notations for the electric dipole moment
Summary
Experiments show that time is not absolute: it flows at different rates depending on an observer's state of motion. This is an example of the strange effects predicted by Einstein's theory of relativity. All of these effects, however, are very small when the relative velocities are small compared to `c`. This makes sense, because Newton's laws have already been thoroughly tested by experiments at such speeds, so a new theory like relativity must agree with the old one in their realm of common applicability. This requirement of backwards-compatibility is known as the correspondence principle.
Since time is not absolute, simultaneity is not a well-defined concept, and therefore the universe cannot operate as Newton imagined, through instantaneous action at a distance. There is a delay in time before a change in the configuration of mass and charge in one corner of the universe will make itself felt as a change in the forces experienced far away. We imagine the outward spread of such a change as a ripple in an invisible universe-filling field of force.
We define the gravitational field at a given point as the force per unit mass exerted on objects inserted at that point, and likewise the electric field is defined as the force per unit charge. These fields are vectors, and the fields generated by multiple sources add according to the rules of vector addition.
When the electric field is constant, the voltage difference between two points lying on a line parallel to the field is related to the field by the equation `DeltaV=-Ed`, where `d` is the distance between the two points.
Fields of force contain energy. The density of energy is proportional to the square of the magnitude of the field. In the case of static fields, we can calculate potential energy either using the previous definition in terms of mechanical work or by calculating the energy stored in the fields. If the fields are not static, the old method gives incorrect results and the new one must be used.
Homework Problems
Key
`sqrt` A computerized answer check is available online.
`int` A problem that requires calculus.
`***` A difficult problem.
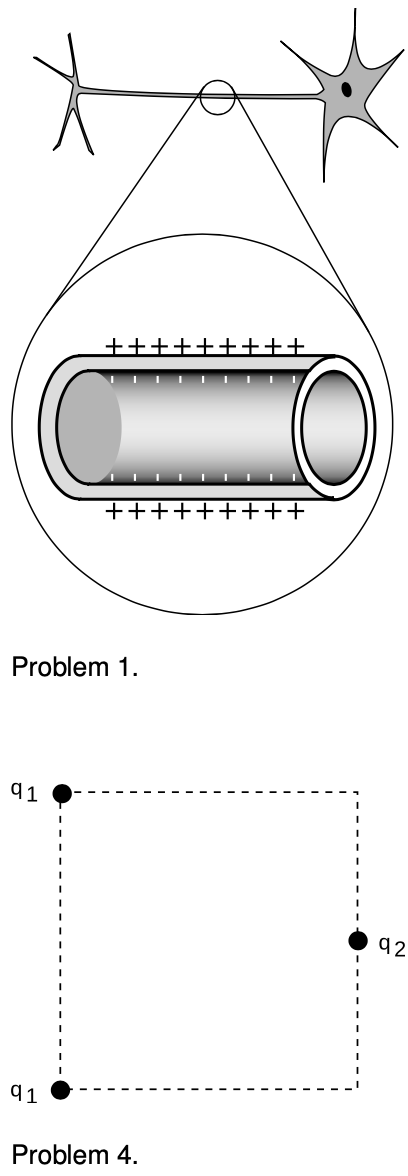 1. In our by-now-familiar neuron, the voltage difference between the inner and outer surfaces of the cell membrane is about `V_"out"-V_"in"=-70 mV` in the resting state, and the thickness of the membrane is about 6.0 nm (i.e., only about a hundred atoms thick). What is the electric field inside the membrane? `sqrt`
1. In our by-now-familiar neuron, the voltage difference between the inner and outer surfaces of the cell membrane is about `V_"out"-V_"in"=-70 mV` in the resting state, and the thickness of the membrane is about 6.0 nm (i.e., only about a hundred atoms thick). What is the electric field inside the membrane? `sqrt`
2. The gap between the electrodes in an automobile engine's spark plug is 0.060 cm. To produce an electric spark in a gasoline-air mixture, an electric field of `3.0×10^6` V/m must be achieved. On starting a car, what minimum voltage must be supplied by the ignition circuit? Assume the field is uniform.`sqrt`
(b) The small size of the gap between the electrodes is inconvenient because it can get blocked easily, and special tools are needed to measure it. Why don't they design spark plugs with a wider gap?
3. (a) At time `t=0`, a positively charged particle is placed, at rest, in a vacuum, in which there is a uniform electric field of magnitude `E`. Write an equation giving the particle's speed, `v`, in terms of `t`, `E`, and its mass and charge `m` and `q`.`sqrt`
(b) If this is done with two different objects and they are observed to have the same motion, what can you conclude about their masses and charges? (For instance, when radioactivity was discovered, it was found that one form of it had the same motion as an electron in this type of experiment.)
4. Three charges are arranged on a square as shown. All three charges are positive. What value of `q_2"/"q_1` will produce zero electric field at the center of the square?
5. Show that the magnitude of the electric field produced by a simple two-charge dipole, at a distant point along the dipole's axis, is to a good approximation proportional to `D"/"r^3`, where `r` is the distance from the dipole. [Hint: Use the approximation`(1+epsilon)^papprox1+pepsilon`, which is valid for small `epsilon`.] `***`
6. Consider the electric field created by a uniform ring of total charge `q` and radius `b`. (a) Show that the field at a point on the ring's axis at a distance `a` from the plane of the ring is `kqa(a^2+b^2)^(-3"/"2)`. (b) Show that this expression has the right behavior for `a=0` and for `a` much greater than `b`. `***`
7. Example 4 on p. 627 showed that the electric field of a long, uniform line of charge falls off with distance as `1"/"r`. By a similar technique, show that the electric field of a uniformly charged plane has no dependence on the distance from the plane. `***`
8. Given that the field of a dipole is proportional to `D"/"r^3` (problem 5), show that its voltage varies as `D"/"r^2`. (Ignore positive and negative signs and numerical constants of proportionality.) `int`
9. A carbon dioxide molecule is structured like O-C-O, with all three atoms along a line. The oxygen atoms grab a little bit of extra negative charge, leaving the carbon positive. The molecule's symmetry, however, means that it has no overall dipole moment, unlike a V-shaped water molecule, for instance. Whereas the voltage of a dipole of magnitude `D` is proportional to `D"/"r^2` (problem 8), it turns out that the voltage of a carbon dioxide molecule along its axis equals `k/r^3`, where `r` is the distance from the molecule and `k` is a constant. What would be the electric field of a carbon dioxide molecule at a distance `r`? `sqrt` `int`
10. A proton is in a region in which the electric field is given by `E=a+bx^3`. If the proton starts at rest at `x_1=0`, find its speed, `v`, when it reaches position `x_2`. Give your answer in terms of `a`, `b`, `x_2`, and `e` and `m`, the charge and mass of the proton. `sqrt` `int`
11. Consider the electric field created by a uniformly charged cylinder that extends to infinity in one direction. (a) Starting from the result of problem 8, show that the field at the center of the cylinder's mouth is `2piksigma`, where `sigma` is the density of charge on the cylinder, in units of coulombs per square meter. [Hint: You can use a method similar to the one in problem 9.] (b) This expression is independent of the radius of the cylinder. Explain why this should be so. For example, what would happen if you doubled the cylinder's radius? `int`
12. In an electrical storm, the cloud and the ground act like a parallel-plate capacitor, which typically charges up due to frictional electricity in collisions of ice particles in the cold upper atmosphere. Lightning occurs when the magnitude of the electric field builds up to a critical value, `E_c`, at which air is ionized.
(a) Treat the cloud as a flat square with sides of length `L`. If it is at a height `h` above the ground, find the amount of energy released in the lightning strike.`sqrt`
(b) Based on your answer from part a, which is more dangerous, a lightning strike from a high-altitude cloud or a low-altitude one?
(c) Make an order-of-magnitude estimate of the energy released by a typical lightning bolt, assuming reasonable values for its size and altitude. `E_c` is about `10^6` V/m.
See problem 16 for a note on how recent research affects this estimate.
 13. The neuron in the figure has been drawn fairly short, but some neurons in your spinal cord have tails (axons) up to a meter long. The inner and outer surfaces of the membrane act as the “plates” of a capacitor. (The fact that it has been rolled up into a cylinder has very little effect.) In order to function, the neuron must create a voltage difference `V` between the inner and outer surfaces of the membrane. Let the membrane's thickness, radius, and length be `t`, `r`, and `L`. (a) Calculate the energy that must be stored in the electric field for the neuron to do its job. (In real life, the membrane is made out of a substance called a dielectric, whose electrical properties increase the amount of energy that must be stored. For the sake of this analysis, ignore this fact.) [Hint: The volume of the membrane is essentially the same as if it was unrolled and flattened out.] `sqrt`
13. The neuron in the figure has been drawn fairly short, but some neurons in your spinal cord have tails (axons) up to a meter long. The inner and outer surfaces of the membrane act as the “plates” of a capacitor. (The fact that it has been rolled up into a cylinder has very little effect.) In order to function, the neuron must create a voltage difference `V` between the inner and outer surfaces of the membrane. Let the membrane's thickness, radius, and length be `t`, `r`, and `L`. (a) Calculate the energy that must be stored in the electric field for the neuron to do its job. (In real life, the membrane is made out of a substance called a dielectric, whose electrical properties increase the amount of energy that must be stored. For the sake of this analysis, ignore this fact.) [Hint: The volume of the membrane is essentially the same as if it was unrolled and flattened out.] `sqrt`
(b) An organism's evolutionary fitness should be better if it needs less energy to operate its nervous system. Based on your answer to part a, what would you expect evolution to do to the dimensions `t` and `r`? What other constraints would keep these evolutionary trends from going too far?
14. To do this problem, you need to understand how to do volume integrals in cylindrical and spherical coordinates. (a) Show that if you try to integrate the energy stored in the field of a long, straight wire, the resulting energy per unit length diverges both at `r->0` and `r->infty`. Taken at face value, this would imply that a certain real-life process, the initiation of a current in a wire, would be impossible, because it would require changing from a state of zero magnetic energy to a state of infinite magnetic energy. (b) Explain why the infinities at `r->0` and `r->infty` don't really happen in a realistic situation. (c) Show that the electric energy of a point charge diverges at `r->0`, but not at `r->infty`.
A remark regarding part (c): Nature does seem to supply us with particles that are charged and pointlike, e.g., the electron, but one could argue that the infinite energy is not really a problem, because an electron traveling around and doing things neither gains nor loses infinite energy; only an infinite change in potential energy would be physically troublesome. However, there are real-life processes that create and destroy pointlike charged particles, e.g., the annihilation of an electron and antielectron with the emission of two gamma rays. Physicists have, in fact, been struggling with infinities like this since about 1950, and the issue is far from resolved. Some theorists propose that apparently pointlike particles are actually not pointlike: close up, an electron might be like a little circular loop of string. `int` `***`
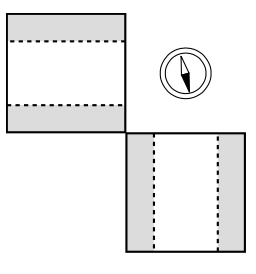
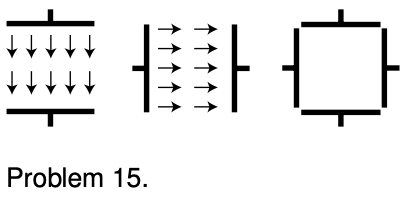 15. The figure shows cross-sectional views of two cubical capacitors, and a cross-sectional view of the same two capacitors put together so that their interiors coincide. A capacitor with the plates close together has a nearly uniform electric field between the plates, and almost zero field outside; these capacitors don't have their plates very close together compared to the dimensions of the plates, but for the purposes of this problem, assume that they still have approximately the kind of idealized field pattern shown in the figure. Each capacitor has an interior volume of `1.00` `m^3`, and is charged up to the point where its internal field is `1.00` V/m. (a) Calculate the energy stored in the electric field of each capacitor when they are separate. (b) Calculate the magnitude of the interior field when the two capacitors are put together in the manner shown. Ignore effects arising from the redistribution of each capacitor's charge under the influence of the other capacitor. (c) Calculate the energy of the put-together configuration. Does assembling them like this release energy, consume energy, or neither? `sqrt`
15. The figure shows cross-sectional views of two cubical capacitors, and a cross-sectional view of the same two capacitors put together so that their interiors coincide. A capacitor with the plates close together has a nearly uniform electric field between the plates, and almost zero field outside; these capacitors don't have their plates very close together compared to the dimensions of the plates, but for the purposes of this problem, assume that they still have approximately the kind of idealized field pattern shown in the figure. Each capacitor has an interior volume of `1.00` `m^3`, and is charged up to the point where its internal field is `1.00` V/m. (a) Calculate the energy stored in the electric field of each capacitor when they are separate. (b) Calculate the magnitude of the interior field when the two capacitors are put together in the manner shown. Ignore effects arising from the redistribution of each capacitor's charge under the influence of the other capacitor. (c) Calculate the energy of the put-together configuration. Does assembling them like this release energy, consume energy, or neither? `sqrt`
16. In problem 12 on p. 645, you estimated the energy released in a bolt of lightning, based on the energy stored in the electric field immediately before the lightning occurs. The assumption was that the field would build up to a certain value, which is what is necessary to ionize air. However, real-life measurements always seemed to show electric fields strengths roughly `10` times smaller than those required in that model. For a long time, it wasn't clear whether the field measurements were wrong, or the model was wrong. Research carried out in 2003 seems to show that the model was wrong. It is now believed that the final triggering of the bolt of lightning comes from cosmic rays that enter the atmosphere and ionize some of the air. If the field is `10` times smaller than the value assumed in problem 12, what effect does this have on the final result of problem 12? `sqrt`
Exercise 22: Field vectors
Apparatus:
- 3 solenoids
- DC power supply
- compass
- ruler
- cut-off plastic cup
At this point you've studied the gravitational field, `g`, and the electric field, `E`, but not the magnetic field, `B`. However, they all have some of the same mathematical behavior: they act like vectors. Furthermore, magnetic fields are the easiest to manipulate in the lab. Manipulating gravitational fields directly would require futuristic technology capable of moving planet-sized masses around! Playing with electric fields is not as ridiculously difficult, but static electric charges tend to leak off through your body to ground, and static electricity effects are hard to measure numerically. Magnetic fields, on the other hand, are easy to make and control. Any moving charge, i.e. any current, makes a magnetic field.
A practical device for making a strong magnetic field is simply a coil of wire, formally known as a solenoid. The field pattern surrounding the solenoid gets stronger or weaker in proportion to the amount of current passing through the wire.
1. With a single solenoid connected to the power supply and laid with its axis horizontal, use a magnetic compass to explore the field pattern inside and outside it. The compass shows you the field vector's direction, but not its magnitude, at any point you choose. Note that the field the compass experiences is a combination (vector sum) of the solenoid's field and the earth's field.
2. What happens when you bring the compass extremely far away from the solenoid?
What does this tell you about the way the solenoid's field varies with distance?
Thus although the compass doesn't tell you the field vector's magnitude numerically, you can get at least some general feel for how it depends on distance.
3. The figure below is a cross-section of the solenoid in the plane containing its axis. Make a sea-of-arrows sketch of the magnetic field in this plane. The length of each arrow should at least approximately reflect the strength of the magnetic field at that point.

Does the field seem to have sources or sinks?
4. What do you think would happen to your sketch if you reversed the wires?
Try it.
5. Now hook up the two solenoids in parallel. You are going to measure what happens when their two fields combine at a certain point in space. As you've seen already, the solenoids' nearby fields are much stronger than the earth's field; so although we now theoretically have three fields involved (the earth's plus the two solenoids'), it will be safe to ignore the earth's field. The basic idea here is to place the solenoids with their axes at some angle to each other, and put the compass at the intersection of their axes, so that it is the same distance from each solenoid. Since the geometry doesn't favor either solenoid, the only factor that would make one solenoid influence the compass more than the other is current. You can use the cut-off plastic cup as a little platform to bring the compass up to the same level as the solenoids' axes.
a) What do you think will happen with the solenoids' axes at 90 degrees to each other, and equal currents? Try it. Now represent the vector addition of the two magnetic fields with a diagram. Check your diagram with your instructor to make sure you're on the right track.
b) Now try to make a similar diagram of what would happen if you switched the wires on one of the solenoids.
After predicting what the compass will do, try it and see if you were right.
c) Now suppose you were to go back to the arrangement you had in part a, but you changed one of the currents to half its former value. Make a vector addition diagram, and use trig to predict the angle.
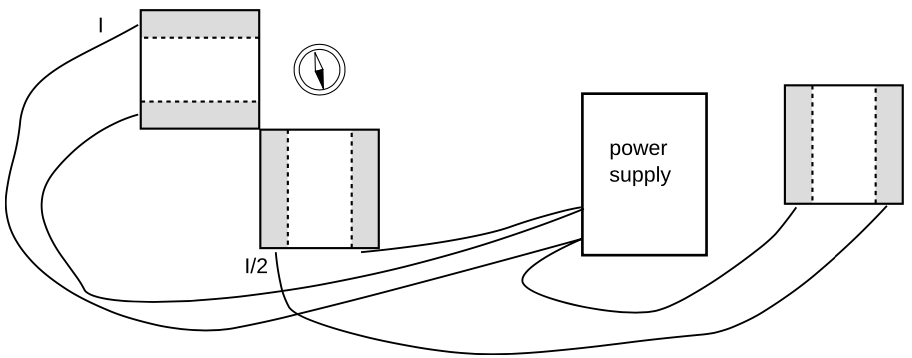
Try it. To cut the current to one of the solenoids in half, an easy and accurate method is simply to put the third solenoid in series with it, and put that third solenoid so far away that its magnetic field doesn't have any significant effect on the compass.
22.9 Summary by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.