22.7 Field lines and Gauss's law by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
22.7 Field lines and Gauss's law (optional)
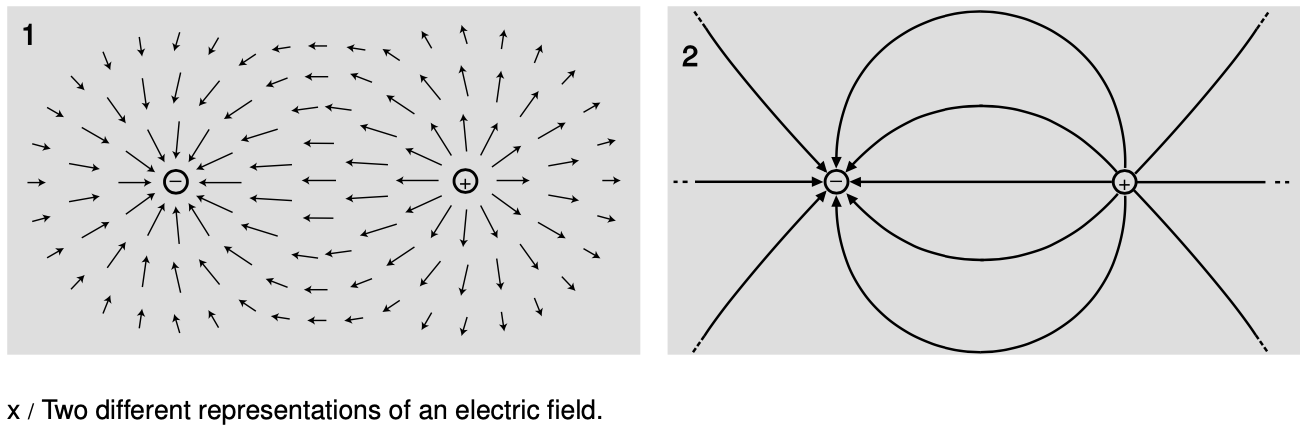
When we look at the “sea of arrows” representation of a field, x/1, there is a natural visual tendency to imagine connecting the arrows as in x/2. The curves formed in this way are called field lines, and they have a direction, shown by the arrowheads.
Example 13: An avalanche transceiver
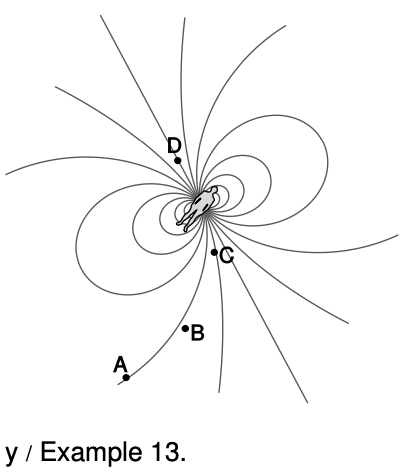 The dipole field pattern is universal: it always has the same mathematical shape, and this holds regardless of whether the field is electric or magnetic, static or oscillating. One of its universal properties is that the field lines always pass through the source, and this is taken advantage of in a device called an avalanche transceiver used by backcountry skiers and hikers in winter. The device is worn on the body and is left in transmitting mode while the user is traveling. It creates a dipole pattern of electric and magnetic fields, oscillating at 457 kHz. If a member of the party is buried in an avalanche, his companions must find and locate him within about 30-90 minutes, or he will suffocate. The rescuers switch their own transceivers to receive mode, allowing them to determine the direction of the field line; when the antenna is parallel to the field line, the oscillating electric field drives electrons up and down it, creating the maximum possible current.
The dipole field pattern is universal: it always has the same mathematical shape, and this holds regardless of whether the field is electric or magnetic, static or oscillating. One of its universal properties is that the field lines always pass through the source, and this is taken advantage of in a device called an avalanche transceiver used by backcountry skiers and hikers in winter. The device is worn on the body and is left in transmitting mode while the user is traveling. It creates a dipole pattern of electric and magnetic fields, oscillating at 457 kHz. If a member of the party is buried in an avalanche, his companions must find and locate him within about 30-90 minutes, or he will suffocate. The rescuers switch their own transceivers to receive mode, allowing them to determine the direction of the field line; when the antenna is parallel to the field line, the oscillating electric field drives electrons up and down it, creating the maximum possible current.
In the figure, the rescuer moves along the field line from A to B. At B, she verifies that the strength of the signal has increased. (If it hadn't, she would have had to turn around and go in the opposite direction.) She redetermines the direction of the field and continues in the new direction. Continuing the process, she proceeds along an approximation to the field line. At D she finds that the field strength has fallen off again, so she knows that she has just passed over the victim's position.
Electric field lines originate from positive charges and terminate on negative ones. We can choose a constant of proportionality that fixes how coarse or fine the “grain of the wood” is, but once this choice is made the strength of each charge is shown by the number of lines that begin or end on it. For example, figure x/2 shows eight lines at each 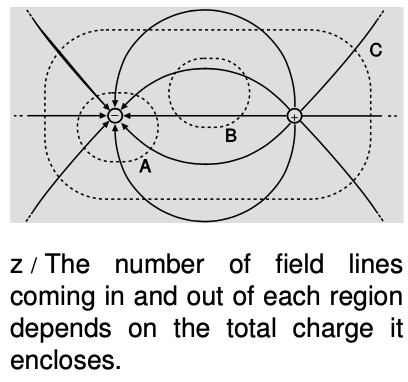 charge, so we know that `q_1"/"q_2=(-8)"/"8=-1`. Because lines never begin or end except on a charge, we can always find the total charge inside any given region by subtracting the number of lines that go in from the number that come out and multiplying by the appropriate constant of proportionality. Ignoring the constant, we can apply this technique to figure z to find `q_A=-8`, `q_B=2-2=0`, and `q_C=5-5=0`.
charge, so we know that `q_1"/"q_2=(-8)"/"8=-1`. Because lines never begin or end except on a charge, we can always find the total charge inside any given region by subtracting the number of lines that go in from the number that come out and multiplying by the appropriate constant of proportionality. Ignoring the constant, we can apply this technique to figure z to find `q_A=-8`, `q_B=2-2=0`, and `q_C=5-5=0`.
Figures x and z are drawn in two dimensions, but we should really imagine them in three dimensions, so that the regions A, B, and C in figure z are volumes bounded by surfaces. It is only because our universe happens to have three dimensions that the field line concept is as useful as it is. This is because the number of field lines per unit area perpendicularly piercing a surface can be interpreted as the strength of the electric field. To see this, consider an imaginary spherical surface of radius `r`, with a positive charge `q` at its center. The field at the surface equals `kq"/"r^2`. The number of field lines piercing the surface is independent of `r`, but the surface's area is proportional to `r^2`, so the number of piercings per unit area is proportional to `1"/"r^2`, just like the electric field. With this interpretation, we arrive at Gauss's law, which states that the field strength on a surface multiplied by the surface area equals the total charge enclosed by the surface. (This particular formulation only works in the case where the field pierces the surface perpendicularly and is constant in magnitude over the whole surface. It can be reformulated so as to eliminate these restrictions, but we won't require that reformulation for our present purposes.)
Example 14: The field of a line of charge
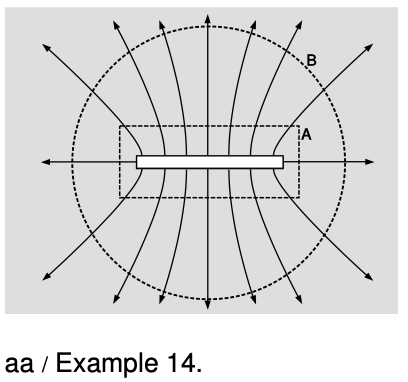 In example 4 on p. 627, we found by simple scaling arguments that the electric field of a line of charge is proportional to `1"/"r`, where `r` is the distance from the line. Since electric fields are always proportional to the Coulomb constant `k` and to the amount of charge, clearly we must have something of the form
In example 4 on p. 627, we found by simple scaling arguments that the electric field of a line of charge is proportional to `1"/"r`, where `r` is the distance from the line. Since electric fields are always proportional to the Coulomb constant `k` and to the amount of charge, clearly we must have something of the form
[4] `E=(...)k(q"/"L)"/"r`, where `q"/"L` is the charge per unit length and `(...)` represents an unknown numerical constant (which you can easily verify is unitless). Using Gauss's law we can fill in the final piece of the puzzle, which is the value of this constant.
Figure aa shows two surfaces, a cylindrical one A and a spherical one B. Every field line that passes through A also passes through B. By making A sufficiently small and B sufficiently large, we can make the field on each surface nearly constant and perpendicular to the surface, as required by our restricted form of Gauss's law. If radius `r_B` is made large, the field at B made by the line of charge becomes indistinguishable from that of a point charge, `kq"/"r_B^2`. By Gauss's law, the electric field at each surface is proportional to the number of field lines divided by its area. But the number of field lines is the same in both cases, so each field is inversely proportional to the corresponding surface area. We therefore have
`E_A=E_B(A_B/A_A)`
`=((kq)/r_B^2)((4pir_B^2)/(2pir_AL))`
`=(2kq)/(Lr_A)`.
The unknown numerical constant equals 2.
Example 15: No charge on the interior of a conductor
I asserted on p. 579 that for a perfect conductor in equilibrium, excess charge is found only at the surface, never in the interior. This can be proved using Gauss's law. Suppose that a charge `q` existed at some point in the interior, and it was in stable equilibrium. For concreteness, let's say `q` is positive. If its equilibrium is to be stable, then we need an electric field everywhere around it that points inward like a pincushion, so that if the charge were to be perturbed slightly, the field would bring it back to its equilibrium position. Since Newton's third law forbids objects from making forces on themselves, this field would have to be the field contributed by all the other charges, not by `q` itself. But by Gauss's law, an external set of charges cannot form this kind of inward-pointing pincushion pattern; for such a pattern, Gauss's law would require there to be some negative charge inside the pincusion.
22.7 Field lines and Gauss's law by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.