22.6 Two or three dimensions by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
22.6 Two or three dimensions
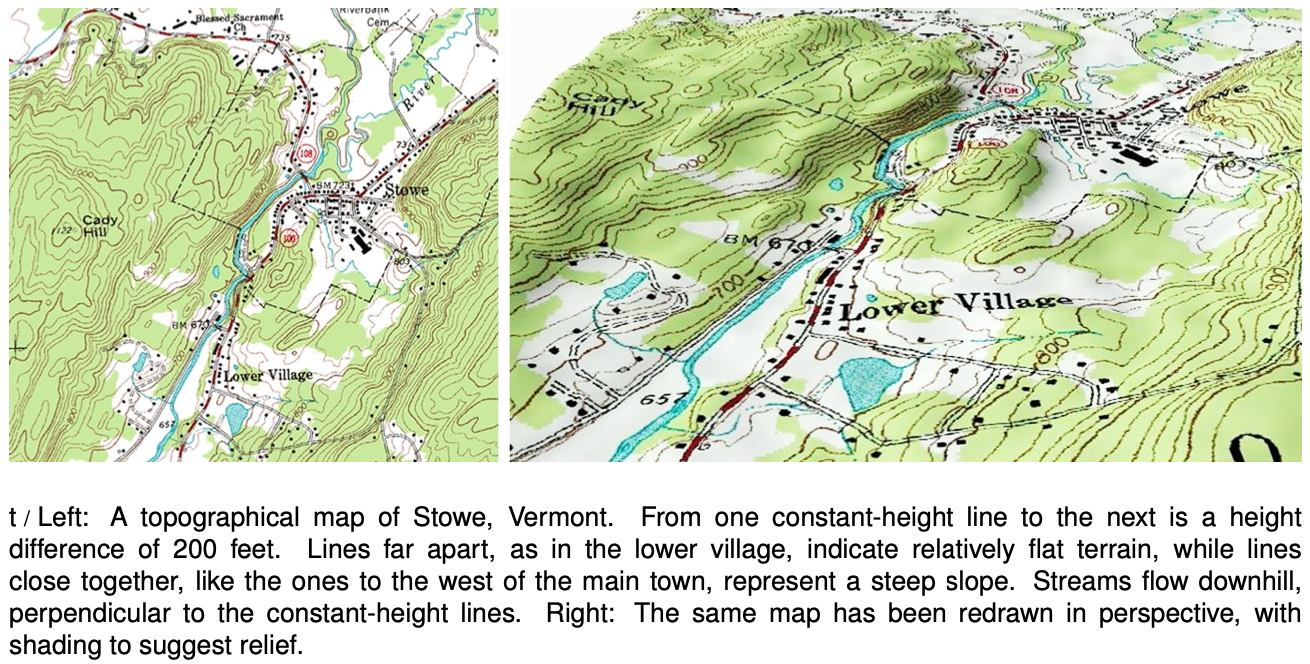
The topographical map shown in figure t suggests a good way to visualize the relationship between field and voltage in two dimensions. Each contour on the map is a line of constant height; some of these are labeled with their elevations in units of feet. Height is related to gravitational potential energy, so in a gravitational analogy, we can think of height as representing voltage. Where the contour lines are far apart, as in the town, the slope is gentle. Lines close together indicate a steep slope.
If we walk along a straight line, say straight east from the town, then height (voltage) is a function of the east-west coordinate `x`. Using the usual mathematical definition of the slope, and writing `V` for the height in order to remind us of the electrical analogy, the slope along such a line is `DeltaV"/"Deltax`. If the slope isn't constant, we either need to use the slope of the `V-x` graph, or use calculus and talk about the derivative `dV"/"dx`.
 What if everything isn't confined to a straight line? Water flows downhill. Notice how the streams on the map cut perpendicularly through the lines of constant height.
What if everything isn't confined to a straight line? Water flows downhill. Notice how the streams on the map cut perpendicularly through the lines of constant height.
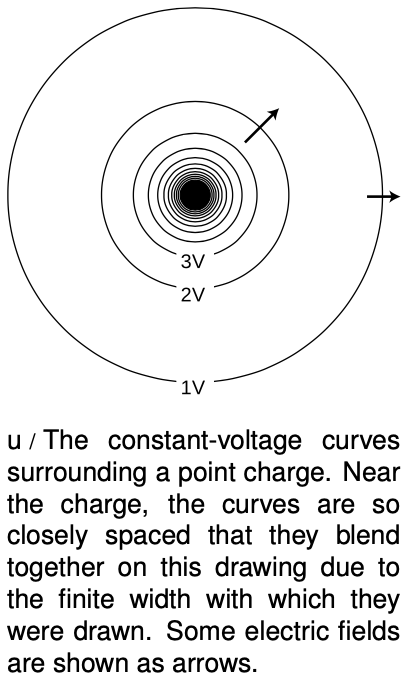
It is possible to map voltages in the same way, as shown in figure u. The electric field is strongest where the constant-voltage curves are closest together, and the electric field vectors always point perpendicular to the constant-voltage curves.
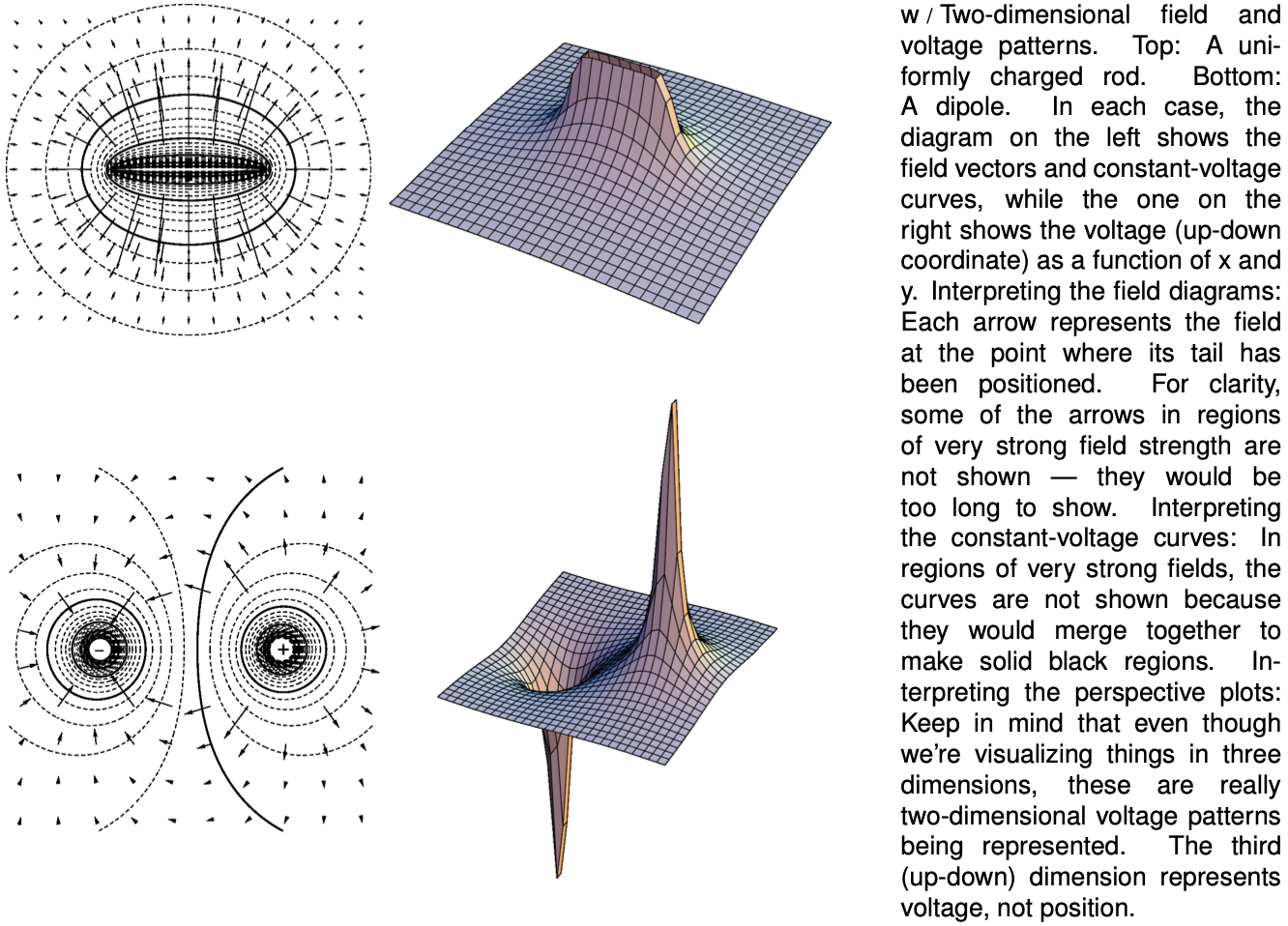
Figure w shows some examples of ways to visualize field and voltage patterns.
Mathematically, the calculus of section 22.5 generalizes to three dimensions as follows:
`E_x=-(dV)/(dx)`
`E_y=-(dV)/(dy)`
`E_z=-(dV)/(dz)`
self-check C:
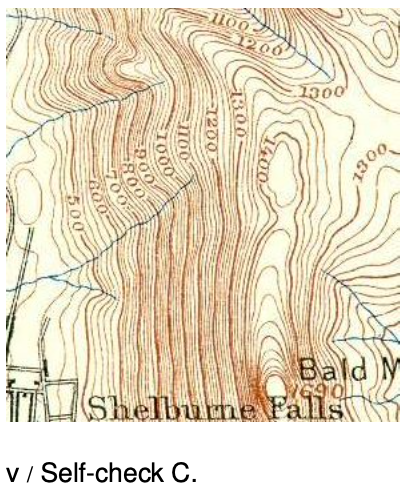 Imagine that the topographical map in figure v represents voltage rather than height. (a) Consider the stream that starts near the center of the map. Determine the positive and negative signs of `dV"/"dx` and `dV"/"dy`, and relate these to the direction of the force that is pushing the current forward against the resistance of friction. (b) If you wanted to find a lot of electric charge on this map, where would you look?
Imagine that the topographical map in figure v represents voltage rather than height. (a) Consider the stream that starts near the center of the map. Determine the positive and negative signs of `dV"/"dx` and `dV"/"dy`, and relate these to the direction of the force that is pushing the current forward against the resistance of friction. (b) If you wanted to find a lot of electric charge on this map, where would you look?
(answer in the back of the PDF version of the book)
22.6 Two or three dimensions by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.