20.2 Quantitative treatment of reflection by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
20.2 Quantitative treatment of reflection (optional)
In this optional section we analyze the reasons why reflections occur at a speed-changing boundary, predict quantitatively the intensities of reflection and transmission, and discuss how to predict for any type of wave which reflections are inverting and which are noninverting. The gory details are likely to be of interest mainly to students with concentrations in the physical sciences, but all readers are encouraged at least to skim the first two subsections for physical insight.
Why reflection occurs
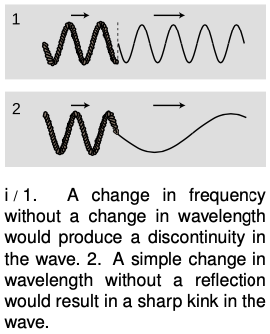 To understand the fundamental reasons for what does occur at the boundary between media, let's first discuss what doesn't happen. For the sake of concreteness, consider a sinusoidal wave on a string. If the wave progresses from a heavier portion of the string, in which its velocity is low, to a lighter-weight part, in which it is high, then the equation tells us that it must change its frequency, or its wavelength, or both. If only the frequency changed, then the parts of the wave in the two different portions of the string would quickly get out of step with each other, producing a discontinuity in the wave, i/1. This is unphysical, so we know that the wavelength must change while the frequency remains constant, 2.
To understand the fundamental reasons for what does occur at the boundary between media, let's first discuss what doesn't happen. For the sake of concreteness, consider a sinusoidal wave on a string. If the wave progresses from a heavier portion of the string, in which its velocity is low, to a lighter-weight part, in which it is high, then the equation tells us that it must change its frequency, or its wavelength, or both. If only the frequency changed, then the parts of the wave in the two different portions of the string would quickly get out of step with each other, producing a discontinuity in the wave, i/1. This is unphysical, so we know that the wavelength must change while the frequency remains constant, 2.
But there is still something unphysical about figure 2. The sudden change in the shape of the wave has resulted in a sharp kink at the boundary. This can't really happen, because the medium tends to accelerate in such a way as to eliminate curvature. A sharp kink corresponds to an infinite curvature at one point, which would produce an infinite acceleration, which would not be consistent with the smooth pattern of wave motion envisioned in figure 2. Waves can have kinks, but not stationary kinks.
We conclude that without positing partial reflection of the wave, we cannot simultaneously satisfy the requirements of (1) continuity of the wave, and (2) no sudden changes in the slope of the wave. (The student who has studied calculus will recognize this as amounting to an assumption that both the wave and its derivative are continuous functions.)
Does this amount to a proof that reflection occurs? Not quite. We have only proven that certain types of wave motion are not valid solutions. In the following subsection, we prove that a valid solution can always be found in which a reflection occurs. Now in physics, we normally assume (but seldom prove formally) that the equations of motion have a unique solution, since otherwise a given set of initial conditions could lead to different behavior later on, but the Newtonian universe is supposed to be deterministic. Since the solution must be unique, and we derive below a valid solution involving a reflected pulse, we will have ended up with what amounts to a proof of reflection.
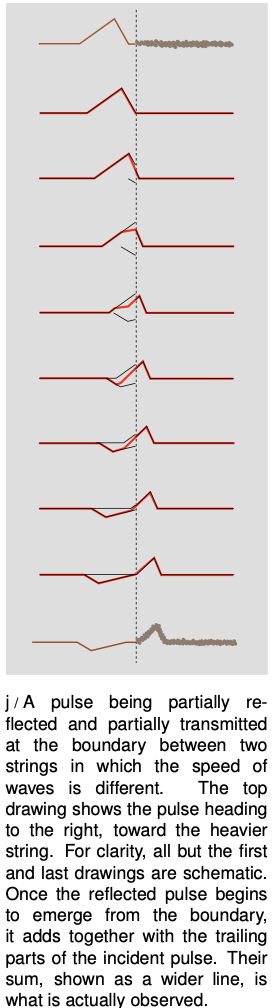 Intensity of reflection
Intensity of reflection
We will now show, in the case of waves on a string, that it is possible to satisfy the physical requirements given above by constructing a reflected wave, and as a bonus this will produce an equation for the proportions of reflection and transmission and a prediction as to which conditions will lead to inverted and which to uninverted reflection. We assume only that the principle of superposition holds, which is a good approximation for waves on a string of sufficiently small amplitude.
Let the unknown amplitudes of the reflected and transmitted waves be `R` and `T`, respectively. An inverted reflection would be represented by a negative value of `R`. We can without loss of generality take the incident (original) wave to have unit amplitude. Superposition tells us that if, for instance, the incident wave had double this amplitude, we could immediately find a corresponding solution simply by doubling `R` and `T`.
Just to the left of the boundary, the height of the wave is given by the height 1 of the incident wave, plus the height `R` of the part of the reflected wave that has just been created and begun heading back, for a total height of `1+R`. On the right side immediately next to the boundary, the transmitted wave has a height `T`. To avoid a discontinuity, we must have
`1+R=T`.
Next we turn to the requirement of equal slopes on both sides of the boundary. Let the slope of the incoming wave be `s` immediately to the left of the junction. If the wave was 100% reflected, and without inversion, then the slope of the reflected wave would be `-s`, since the wave has been reversed in direction. In general, the slope of the reflected wave equals `-sR`, and the slopes of the superposed waves on the left side add up to `s-sR`. On the right, the slope depends on the amplitude, `T`, but is also changed by the stretching or compression of the wave due to the change in speed. If, for example, the wave speed is twice as great on the right side, then the slope is cut in half by this effect. The slope on the right is therefore `s(v_1"/"v_2)T`, where `v_1` is the velocity in the original medium and `v_2` the velocity in the new medium. Equality of slopes gives `s-sR=s(v_1"/"v_2)T`, or
`1-R=v_1/v_2T.`
Solving the two equations for the unknowns `R` and `T` gives
`R=(v_2-v_1)/(v_2 + v_1)` and `T=(2v_2)/(v_2 +v_1`.
The first equation shows that there is no reflection unless the two wave speeds are different, and that the reflection is inverted in reflection back into a fast medium.
The energies of the transmitted and reflected waves always add up to the same as the energy of the original wave. There is never any abrupt loss (or gain) in energy when a wave crosses a boundary. (Conversion of wave energy to heat occurs for many types of waves, but it occurs throughout the medium.) The equation for `T`, surprisingly, allows the amplitude of the transmitted wave to be greater than 1, i.e., greater than that of the incident wave. This does not violate conservation of energy, because this occurs when the second string is less massive, reducing its kinetic energy, and the transmitted pulse is broader and less strongly curved, which lessens its potential energy.
 Inverted and uninverted reflections in general
Inverted and uninverted reflections in general
For waves on a string, reflections back into a faster medium are inverted, while those back into a slower medium are uninverted. Is this true for all types of waves? The rather subtle answer is that it depends on what property of the wave you are discussing.
Let's start by considering wave disturbances of freeway traffic. Anyone who has driven frequently on crowded freeways has observed the phenomenon in which one driver taps the brakes, starting a chain reaction that travels backward down the freeway as each person in turn exercises caution in order to avoid rear-ending anyone. The reason why this type of wave is relevant is that it gives a simple, easily visualized example of how our description of a wave depends on which aspect of the wave we have in mind. In steadily flowing freeway traffic, both the density of cars and their velocity are constant all along the road. Since there is no disturbance in this pattern of constant velocity and density, we say that there is no wave. Now if a wave is touched off by a person tapping the brakes, we can either describe it as a region of high density or as a region of decreasing velocity.
The freeway traffic wave is in fact a good model of a sound wave, and a sound wave can likewise be described either by the density (or pressure) of the air or by its speed. Likewise many other types of waves can be described by either of two functions, one of which is often the derivative of the other with respect to position.
Now let's consider reflections. If we observe the freeway wave in a mirror, the high-density area will still appear high in density, but velocity in the opposite direction will now be described by a negative number. A person observing the mirror image will draw the same density graph, but the velocity graph will be flipped across the `x` axis, and its original region of negative slope will now have positive slope. Although I don't know any physical situation that would correspond to the reflection of a traffic wave, we can immediately apply the same reasoning to sound waves, which often do get reflected, and determine that a reflection can either be density-inverting and velocity-noninverting or density-noninverting and velocity-inverting.
This same type of situation will occur over and over as one encounters new types of waves, and to apply the analogy we need only determine which quantities, like velocity, become negated in a mirror image and which, like density, stay the same.
A light wave, for instance, consists of a traveling pattern of electric and magnetic fields. All you need to know in order to analyze the reflection of light waves is how electric and magnetic fields behave under reflection; you don't need to know any of the detailed physics of electricity and magnetism. An electric field can be detected, for example, by the way one's hair stands on end. The direction of the hair indicates the direction of the electric field. In a mirror image, the hair points the other way, so the electric field is apparently reversed in a mirror image. The behavior of magnetic fields, however, is a little tricky. The magnetic properties of a bar magnet, for instance, are caused by the aligned rotation of the outermost orbiting electrons of the atoms. In a mirror image, the direction of rotation is reversed, say from clockwise to counterclockwise, and so the magnetic field is reversed twice: once simply because the whole picture is flipped and once because of the reversed rotation of the electrons. In other words, magnetic fields do not reverse themselves in a mirror image. We can thus predict that there will be two possible types of reflection of light waves. In one, the electric field is inverted and the magnetic field uninverted (example 8, p. 690). In the other, the electric field is uninverted and the magnetic field inverted.
20.2 Quantitative treatment of reflection by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.