19.4 Periodic waves by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
19.4 Periodic waves
Period and frequency of a periodic wave
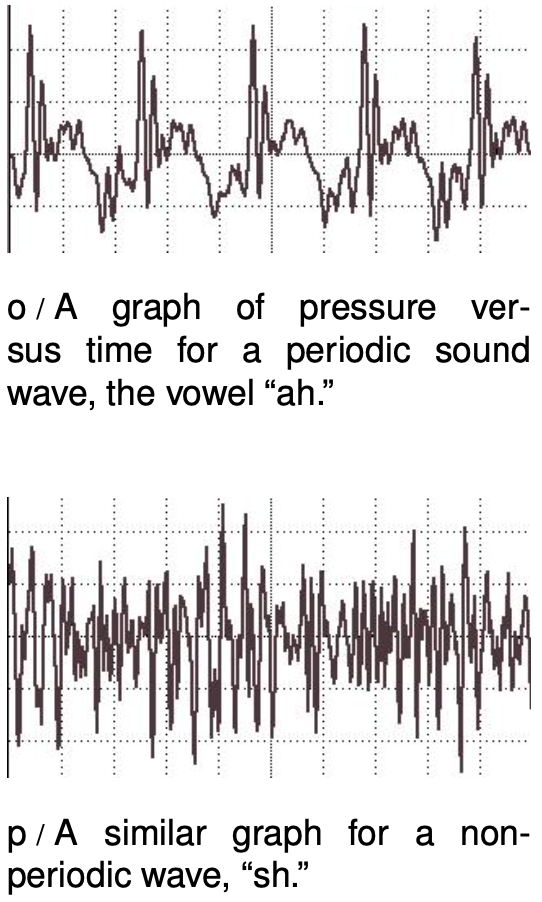 You choose a radio station by selecting a certain frequency. We have already defined period and frequency for vibrations, but what do they signify in the case of a wave? We can recycle our previous definition simply by stating it in terms of the vibrations that the wave causes as it passes a receiving instrument at a certain point in space. For a sound wave, this receiver could be an eardrum or a microphone. If the vibrations of the eardrum repeat themselves over and over, i.e., are periodic, then we describe the sound wave that caused them as periodic. Likewise we can define the period and frequency of a wave in terms of the period and frequency of the vibrations it causes. As another example, a periodic water wave would be one that caused a rubber duck to bob in a periodic manner as they passed by it.
You choose a radio station by selecting a certain frequency. We have already defined period and frequency for vibrations, but what do they signify in the case of a wave? We can recycle our previous definition simply by stating it in terms of the vibrations that the wave causes as it passes a receiving instrument at a certain point in space. For a sound wave, this receiver could be an eardrum or a microphone. If the vibrations of the eardrum repeat themselves over and over, i.e., are periodic, then we describe the sound wave that caused them as periodic. Likewise we can define the period and frequency of a wave in terms of the period and frequency of the vibrations it causes. As another example, a periodic water wave would be one that caused a rubber duck to bob in a periodic manner as they passed by it.
The period of a sound wave correlates with our sensory impression of musical pitch. A high frequency (short period) is a high note. The sounds that really define the musical notes of a song are only the ones that are periodic. It is not possible to sing a non-periodic sound like “sh” with a definite pitch.
The frequency of a light wave corresponds to color. Violet is the high-frequency end of the rainbow, red the low-frequency end. A color like brown that does not occur in a rainbow is not a periodic light wave. Many phenomena that we do not normally think of as light are actually just forms of light that are invisible because they fall outside the range of frequencies our eyes can detect. Beyond the red end of the visible rainbow, there are infrared and radio waves. Past the violet end, we have ultraviolet, x-rays, and gamma rays.
Graphs of waves as a function of position
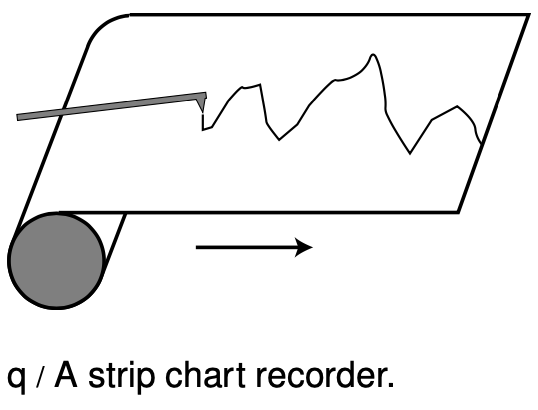 Some waves, like sound waves, are easy to study by placing a detector at a certain location in space and studying the motion as a function of time. The result is a graph whose horizontal axis is time. With a water wave, on the other hand, it is simpler just to look at the wave directly. This visual snapshot amounts to a graph of the height of the water wave as a function of position. Any wave can be represented in either way.
Some waves, like sound waves, are easy to study by placing a detector at a certain location in space and studying the motion as a function of time. The result is a graph whose horizontal axis is time. With a water wave, on the other hand, it is simpler just to look at the wave directly. This visual snapshot amounts to a graph of the height of the water wave as a function of position. Any wave can be represented in either way.
An easy way to visualize this is in terms of a strip chart recorder, an obsolescing device consisting of a pen that wiggles back and forth as a roll of paper is fed under it. It can be used to record a person's electrocardiogram, or seismic waves too small to be felt as a noticeable earthquake but detectable by a seismometer. Taking the seismometer as an example, the chart is essentially a record of the ground's wave motion as a function of time, but if the paper was set to feed at the same velocity as the motion of an earthquake wave, it would also be a full-scale representation of the profile of the actual wave pattern itself. Assuming, as is usually the case, that the wave velocity is a constant number regardless of the wave's shape, knowing the wave motion as a function of time is equivalent to knowing it as a function of position.
Wavelength
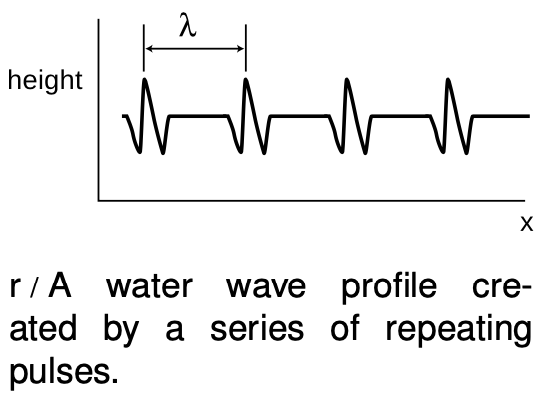 Any wave that is periodic will also display a repeating pattern when graphed as a function of position. The distance spanned by one repetition is referred to as one wavelength. The usual notation for wavelength is `lambda`, the Greek letter lambda. Wavelength is to space as period is to time.
Any wave that is periodic will also display a repeating pattern when graphed as a function of position. The distance spanned by one repetition is referred to as one wavelength. The usual notation for wavelength is `lambda`, the Greek letter lambda. Wavelength is to space as period is to time.

Wave velocity related to frequency and wavelength
This important and useful relationship is more commonly written in terms of the frequency, `v=flambda`.
Example 5: Wavelength of radio waves
- The speed of light is `3.0×10^8 m"/"s`. What is the wavelength of the radio waves emitted by KMHD, a station whose frequency is 89.1 MHz?
- Solving for wavelength, we have
`lambda=v/f`
`=(3.0×10^8 m`/`s)`/`(89.1×10^6 s^(-1))`
`=3.4 m`
The size of a radio antenna is closely related to the wavelength of the waves it is intended to receive. The match need not be exact (since after all one antenna can receive more than one wavelength!), but the ordinary “whip” antenna such as a car's is 1/4 of a wavelength. An antenna optimized to receive KMHD's signal would have a length of `3.4 m`/`4=0.85 m`.
 The equation `v=flambda` defines a fixed relationship between any two of the variables if the other is held fixed. The speed of radio waves in air is almost exactly the same for all wavelengths and frequencies (it is exactly the same if they are in a vacuum), so there is a fixed relationship between their frequency and wavelength. Thus we can say either “Are we on the same wavelength?” or “Are we on the same frequency?”
The equation `v=flambda` defines a fixed relationship between any two of the variables if the other is held fixed. The speed of radio waves in air is almost exactly the same for all wavelengths and frequencies (it is exactly the same if they are in a vacuum), so there is a fixed relationship between their frequency and wavelength. Thus we can say either “Are we on the same wavelength?” or “Are we on the same frequency?”
A different example is the behavior of a wave that travels from a region where the medium has one set of properties to an area where the medium behaves differently. The frequency is now fixed, because otherwise the two portions of the wave would otherwise get out of step, causing a kink or discontinuity at the boundary, which would be unphysical. (A more careful argument is that a kink or discontinuity would have infinite curvature, and waves tend to flatten out their curvature. An infinite curvature would flatten out infinitely fast, i.e., it could never occur in the first place.) Since the frequency must stay the same, any change in the velocity that results from the new medium must cause a change in wavelength.
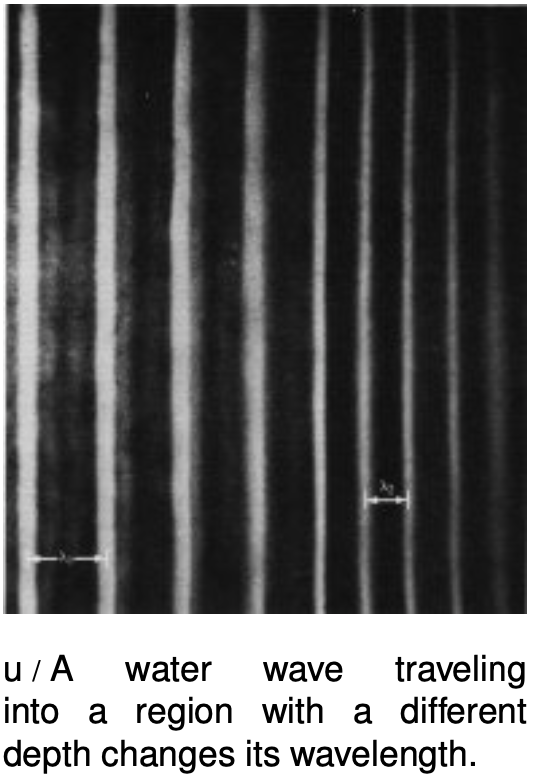
The velocity of water waves depends on the depth of the water, so based on `lambda=v/f`, we see that water waves that move into a region of different depth must change their wavelength, as shown in figure u. This effect can be observed when ocean waves come up to the shore. If the deceleration of the wave pattern is sudden enough, the tip of the wave can curl over, resulting in a breaking wave.
A note on dispersive waves
The discussion of wave velocity given here is actually an oversimplification for a wave whose velocity depends on its frequency and wavelength. Such a wave is called a dispersive wave. Nearly all the waves we deal with in this course are non-dispersive, but the issue becomes important in quantum physics, as discussed in more detail in optional section 35.2.
Sinusoidal waves
Sinusoidal waves are the most important special case of periodic waves. In fact, many scientists and engineers would be uncomfortable with defining a waveform like the “ah” vowel sound as having a definite frequency and wavelength, because they consider only sine waves to be pure examples of a certain frequency and wavelengths. Their bias is not unreasonable, since the French mathematician Fourier showed that any periodic wave with frequency `f` can be constructed as a superposition of sine waves with frequencies `f, 2f, 3f, ...` In this sense, sine waves are the basic, pure building blocks of all waves. (Fourier's result so surprised the mathematical community of France that he was ridiculed the first time he publicly presented his theorem.)
However, what definition to use is a matter of utility. Our sense of hearing perceives any two sounds having the same period as possessing the same pitch, regardless of whether they are sine waves or not. This is undoubtedly because our ear-brain system evolved to be able to interpret human speech and animal noises, which are periodic but not sinusoidal. Our eyes, on the other hand, judge a color as pure (belonging to the rainbow set of colors) only if it is a sine wave.
Discussion Question
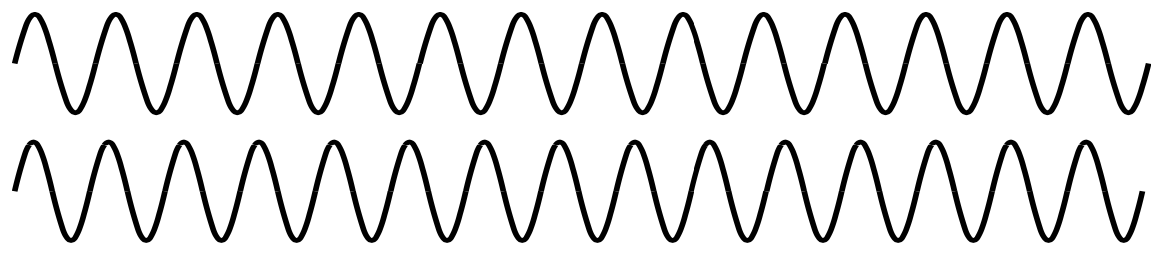
A Suppose we superimpose two sine waves with equal amplitudes but slightly different frequencies, as shown in the figure. What will the superposition look like? What would this sound like if they were sound waves?
19.4 Periodic waves by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.