18.2 Energy lost from vibrations by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
18.2 Energy lost from vibrations
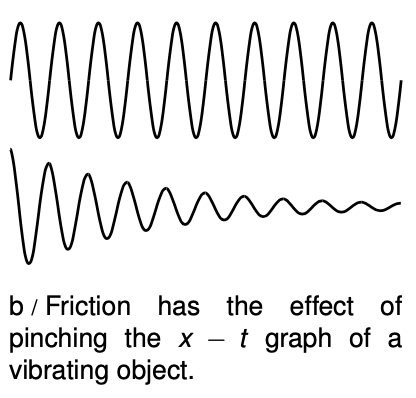 Until now, we have been making the relatively unrealistic assumption that a vibration would never die out. For a realistic mass on a spring, there will be friction, and the kinetic and potential energy of the vibrations will therefore be gradually converted into heat. Similarly, a guitar string will slowly convert its kinetic and potential energy into sound. In all cases, the effect is to “pinch” the sinusoidal `x-t` graph more and more with passing time. Friction is not necessarily bad in this context --- a musical instrument that never got rid of any of its energy would be completely silent! The dissipation of the energy in a vibration is known as damping.
Until now, we have been making the relatively unrealistic assumption that a vibration would never die out. For a realistic mass on a spring, there will be friction, and the kinetic and potential energy of the vibrations will therefore be gradually converted into heat. Similarly, a guitar string will slowly convert its kinetic and potential energy into sound. In all cases, the effect is to “pinch” the sinusoidal `x-t` graph more and more with passing time. Friction is not necessarily bad in this context --- a musical instrument that never got rid of any of its energy would be completely silent! The dissipation of the energy in a vibration is known as damping.
self-check:
Most people who try to draw graphs like those shown on the left will tend to shrink their wiggles horizontally as well as vertically. Why is this wrong?
(answer in the back of the PDF version of the book)
In the graphs in figure `b`, I have not shown any point at which the damped vibration finally stops completely. Is this realistic? Yes and no. If energy is being lost due to friction between two solid surfaces, then we expect the force of friction to be nearly independent of velocity. This constant friction force puts an upper limit on the total distance that the vibrating object can ever travel without replenishing its energy, since work equals force times distance, and the object must stop doing work when its energy is all converted into heat. (The friction force does reverse directions when the object turns around, but reversing the direction of the motion at the same time that we reverse the direction of the force makes it certain that the object is always doing positive work, not negative work.)
Damping due to a constant friction force is not the only possibility however, or even the most common one. A pendulum may be damped mainly by air friction, which is approximately proportional to `v^2`, while other systems may exhibit friction forces that are proportional to `v`. It turns out that friction proportional to `v` is the simplest case to analyze mathematically, and anyhow all the important physical insights can be gained by studying this case.
If the friction force is proportional to `v`, then as the vibrations die down, the frictional forces get weaker due to the lower speeds. The less energy is left in the system, the more miserly the system becomes with giving away any more energy. Under these conditions, the vibrations theoretically never die out completely, and mathematically, the loss of energy from the system is exponential: the system loses a fixed percentage of its energy per cycle. This is referred to as exponential decay.
A non-rigorous proof is as follows. The force of friction is proportional to `v`, and` v`" is proportional to how far the object travels in one cycle, so the frictional force is proportional to amplitude. The amount of work done by friction is proportional to the force and to the distance traveled, so the work done in one cycle is proportional to the square of the amplitude. Since both the work and the energy are proportional to `A^2`, the amount of energy taken away by friction in one cycle is a fixed percentage of the amount of energy the system has.
 self-check:
self-check:
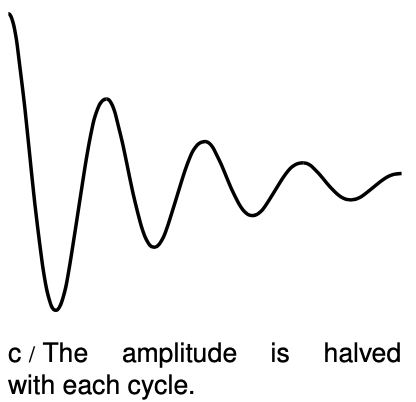
Figure c shows an `x-t` graph for a strongly damped vibration, which loses half of its amplitude with every cycle. What fraction of the energy is lost in each cycle?
(answer in the back of the PDF version of the book)
It is customary to describe the amount of damping with a quantity called the quality factor, `Q`, defined as the number of cycles required for the energy to fall off by a factor of 535. (The origin of this obscure numerical factor is `e^(2pi)`, where `e=2.71828...`is the base of natural logarithms. Choosing this particular number causes some of our later equations to come out nice and simple.) The terminology arises from the fact that friction is often considered a bad thing, so a mechanical device that can vibrate for many oscillations before it loses a significant fraction of its energy would be considered a high-quality device.
Example 3: Exponential decay in a trumpet
- The vibrations of the air column inside a trumpet have a `Q` of about 10. This means that even after the trumpet player stops blowing, the note will keep sounding for a short time. If the player suddenly stops blowing, how will the sound intensity 20 cycles later compare with the sound intensity while she was still blowing?
- The trumpet's `Q` is 10, so after 10 cycles the energy will have fallen off by a factor of 535. After another 10 cycles we lose another factor of 535, so the sound intensity is reduced by a factor of `535×535=2.9×10^5`.
The decay of a musical sound is part of what gives it its character, and a good musical instrument should have the right `Q`, but the `Q` that is considered desirable is different for different instruments. A guitar is meant to keep on sounding for a long time after a string has been plucked, and might have a `Q` of 1000 or 10000. One of the reasons why a cheap synthesizer sounds so bad is that the sound suddenly cuts off after a key is released.
Example 4: `Q` of a stereo speaker
Stereo speakers are not supposed to reverberate or “ring” after an electrical signal that stops suddenly. After all, the recorded music was made by musicians who knew how to shape the decays of their notes correctly. Adding a longer “tail” on every note would make it sound wrong. We therefore expect that stereo speaker will have a very low `Q`, and indeed, most speakers are designed with a `Q` of about 1. (Low-quality speakers with larger `Q` values are referred to as “boomy.”)
We will see later in the chapter that there are other reasons why a speaker should not have a high `Q`.
18.2 Energy lost from vibrations by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.