18.1 Energy in vibrations by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.
18.1 Energy in vibrations
One way of describing the collapse of the bridge is that the bridge kept taking energy from the steadily blowing wind and building up more and more energetic vibrations. In this section, we discuss the energy contained in a vibration, and in the subsequent sections we will move on to the loss of energy and the adding of energy to a vibrating system, all with the goal of understanding the important phenomenon of resonance.
Going back to our standard example of a mass on a spring, we find that there are two forms of energy involved: the potential energy stored in the spring and the kinetic energy of the moving mass. We may start the system in motion either by hitting the mass to put in kinetic energy or by pulling it to one side to put in potential energy. Either way, the subsequent behavior of the system is identical. It trades energy back and forth between kinetic and potential energy. (We are still assuming there is no friction, so that no energy is converted to heat, and the system never runs down.)
The most important thing to understand about the energy content of vibrations is that the total energy is proportional to the square of the amplitude. Although the total energy is constant, it is instructive to consider two specific moments in the motion of the mass on a spring as examples. When the mass is all the way to one side, at rest and ready to reverse directions, all its energy is potential. We have already seen that the potential energy stored in a spring equals `(1/2)kx^2`, so the energy is proportional to the square of the amplitude. Now consider the moment when the mass is passing through the equilibrium point at `x=0`. At this point it has no potential energy, but it does have kinetic energy. The velocity is proportional to the amplitude of the motion, and the kinetic energy, `KE=(1/2)mv^2`, is proportional to the square of the velocity, so again we find that the energy is proportional to the square of the amplitude. The reason for singling out these two points is merely instructive; proving that energy is proportional to `A^2` at any point would suffice to prove that energy is proportional to `A^2` in general, since the energy is constant.
Are these conclusions restricted to the mass-on-a-spring example? No. We have already seen that `F_X=-kx` is a valid approximation for any vibrating object, as long as the amplitude is small. We are thus left with a very general conclusion: the energy of any vibration is approximately proportional to the square of the amplitude, provided that the amplitude is small.
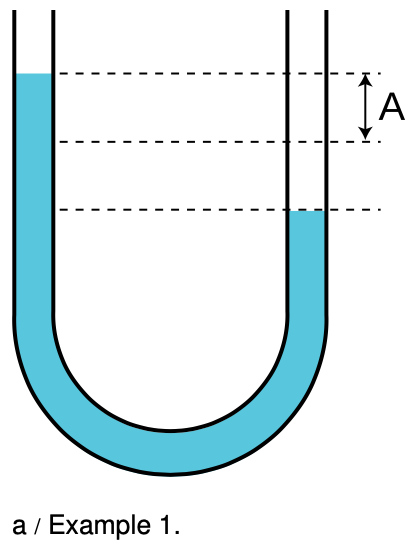 Example 1: Water in a U-tube
Example 1: Water in a U-tube
If water is poured into a U-shaped tube as shown in the figure, it can undergo vibrations about equilibrium. The energy of such a vibration is most easily calculated by considering the “turnaround point” when the water has stopped and is about to reverse directions. At this point, it has only potential energy and no kinetic energy, so by calculating its potential energy we can find the energy of the vibration. This potential energy is the same as the work that would have to be done to take the water out of the right-hand side down to a depth `A` below the equilibrium level, raise it through a height `A`, and place it in the left-hand side. The weight of this chunk of water is proportional to `A`, and so is the height through which it must be lifted, so the energy is proportional to `A^2`.
Example 2: The range of energies of sound waves
- The amplitude of vibration of your eardrum at the threshold of pain is about `10^6` times greater than the amplitude with which it vibrates in response to the softest sound you can hear. How many times greater is the energy with which your ear has to cope for the painfully loud sound, compared to the soft sound?
- The amplitude is `10^6` times greater, and energy is proportional to the square of the amplitude, so the energy is greater by a factor of `10^12` . This is a phenomenally large factor!
We are only studying vibrations right now, not waves, so we are not yet concerned with how a sound wave works, or how the energy gets to us through the air. Note that because of the huge range of energies that our ear can sense, it would not be reasonable to have a sense of loudness that was additive. Consider, for instance, the following three levels of sound:
| barely audible wind |
| quiet conversation .......`10^5` times more energy than the wind |
| heavy metal concert .....`10^12` times more energy than the wind |
In terms of addition and subtraction, the difference between the wind and the quiet conversation is nothing compared to the difference between the quiet conversation and the heavy metal concert. Evolution wanted our sense of hearing to be able to encompass all these sounds without collapsing the bottom of the scale so that anything softer than the crack of doom would sound the same. So rather than making our sense of loudness additive, mother nature made it multiplicative. We sense the difference between the wind and the quiet conversation as spanning a range of about 5/12 as much as the whole range from the wind to the heavy metal concert. Although a detailed discussion of the decibel scale is not relevant here, the basic point to note about the decibel scale is that it is logarithmic. The zero of the decibel scale is close to the lower limit of human hearing, and adding 1 unit to the decibel measurement corresponds to multiplying the energy level (or actually the power per unit area) by a certain factor.
18.1 Energy in vibrations by Benjamin Crowell, Light and Matter licensed under the Creative Commons Attribution-ShareAlike license.